【编译原理】重学笔记
2023/12/23大约 14 分钟
【编译原理】重学笔记
目录
词法分析
基本概念
编译程序是一种翻译程序,将源语言翻译成目标语言
基本步骤
- 词法分析
- 语法分析
- 语义分析
- 中间代码生成(优化)
- 目标代码生成(优化)
几个概念
字母表: Σ = {a,b,c}
符号串: 字母表Σ= {a,b,c}中任意元素的任意组合:a,ab,aac
空串: 空的符号串,ε
子串: 对于符号串x=abc,a,ab,abc都是其子串,ba,ε都不是
符号串长度: |ab|=2 |ε|=0
符号串的头尾
- 对于符号串
z=xy,- 看成两部分组成
- 如果x是z的头,那么y是z的尾
- 若x非空(头非空),则y为固有尾
- 若y非空(尾非空),则x为固有头
- 对于符号串
z=abc,- 头:
ε,a,ab,abc, - 尾:
ε,c,bc,abc - 如果把
abc看做头,那么尾就是ε,所以abc就不是固有头(因为上面说了,尾是非空,头才能是固有头),固有头应当是ε,a,ab, - 如果把
abc看做尾,那么头就是ε,所以abc就不是固有尾,固有尾应当是ε,b,ab,
- 头:
- 省略写法:
- 省略不感兴趣的部分
z=...x...z=x...
我的总结
上面这段是把书上的说法结构化之后又添加了点解释,但还是太废话了,总的来说,
应该就是可以把符号串看成两部分,前一部分可以称作头,后一部分可以称作尾,
但是只有当头为非空时,尾才能称之为固有尾,只有当尾为非空时,头才能被称为固有头
符号串的连接
- 设有符号串
x=ST y=abu - 则他们的连接为:
xy=STabu - 显然:
εx=xε=x|x|=2 |y|=3 |xy|=5
符号串的方幂
符号串的集合
- 集合
A由符号串组成,且这些符号串全部由同一个字母表Σ组成。A = {1,12,123} Σ={1,2,3}
- 表示法:
- 枚举表示法:
A = {1,11,111} - 省略表示法:
B = {1,11,111,...}(如果有规律的话) - 概述表示法:
C = { X | X满足条件C }A = { X | X是字母表Σ={1}上的符号串,且1<=|X|<=3 }
- 枚举表示法:
- 空符号串集:
A= {} = ∅,没有任何符号串,连空串也没有的符号串的集合 - 两符号串集合的乘积:
- 就是将两集合的符号串连接起来。
AB表示的是符号串集合的乘积xy表示的是符号串的连接
- 案例
A={12,34} B={45,67}AB={1245,1267,3445,3467}
字母表的闭包运算
Σ*表示字母表Σ上一切长度为n(n>=0)的字符串所组成的集合- 案例
Σ={1,2,3}
Σ*={
ε,
1,2,3
11,12,13,21,22,23,31,32,33,
...
}字母表的正闭包
Σ*表示字母表Σ上一切长度为n(n>0)的字符串所组成的集合- 显然:
- 他和闭包运算相差了一个零次幂:
- 他的每一项的系数和闭包运算相差了一个Σ:
- 他和闭包运算相差了一个零次幂:
文法和语言
产生式(重写规则)
- 元语言符号
->和::=都表示定义为|,表示或者
- 左部,
->和::=左侧的部分- 统统都是非终结符
- 右部,
->和::=右侧的部分- 可能是非终结符,也可能是终结符
上下文无关的文法
- 标准定义是一个四元组
- 非终结符集合
- 终结符集合
- 重写规则集合
- 识别符号
- 字汇表:
- 显然
- 非终极符和终结符的交集为空集
- 非终极符和终结符的交集为空集
完整写法案例
有
文法G = (V_N,V_T,P,S)
其中
非终结符集合 V_N = {a,b,c,...,z,0,1,2,...,9}
终结符集合 V_T = {<标识符>,<字母>,<数字>}
重写规则集合 P = {
<标识符> -> <字母>
<标识符> -> <标识符><数字>
<字母> -> a|b|c|...|z
<数字> -> 0|1|2|...|9
}
识别符号 S = <标识符>简化写法案例
- 很多时候只需要写出文法的产生式,不需要写出完整的四元组。
- 一般约定第一条产生式的左部为识别符
- 尖括号为非终结符,否则为终结符
- 或者大写字母表示非终结符,小写字母为非终结符
- 另外,也可以把
G写成G[识别符]
文法G[<标识符>]:
<标识符> -> <字母>
<标识符> -> <标识符><数字>
<字母> -> a|b|c|...|z
<数字> -> 0|1|2|...|9推导和规约
- 若
v=123<字母>321<字母>:=aw=123a321
- 则称:
- v直接推导(产生出)w 记作
- w直接规约到v 记作
- v直接推导(产生出)w 记作
- 注意区分规约符号
推导长度
1通过直接推导出一个新的字符串0通过直接推导,推导出本身- 多步推导:
- 广义推导:
文法描述的语言
- 若有
文法G[开始符号Z] 字汇表V - 如果:
- (由开始符号,经过广义推导,推导出x,且x属于字汇表上的闭包,则称x是句型,由非终结符和终结符组成)
- 如果:
- (由开始符号,经过广义推导,推导出x,且x属于字汇表终结符闭包,则称x是句子,由终结符组成)
- 显然,根据定义,句型包含句子,句子是一种特殊的句型。
文法表述的语言
- 文法表述的语言L,是该文法一切句子的集合。
递归规则
- 文法产生式的右部出现在了左部
- 左递归:文法产生式的右部出现在左部,且出现在右部的开头
<标识符> -> <标识符><数字>
- 左递归:文法产生式的右部出现在左部,且出现在右部的结尾
<标识符> -> <数字><标识符>
- 普通的递归规则,既不出现在右部的开头也不出现在左部结尾
文法与语言
一个文法只能唯一描述一中语言,但一个语言可以用多种文法来描述。
如果两个文法描述了同一种语言
乔姆斯基语言分类法
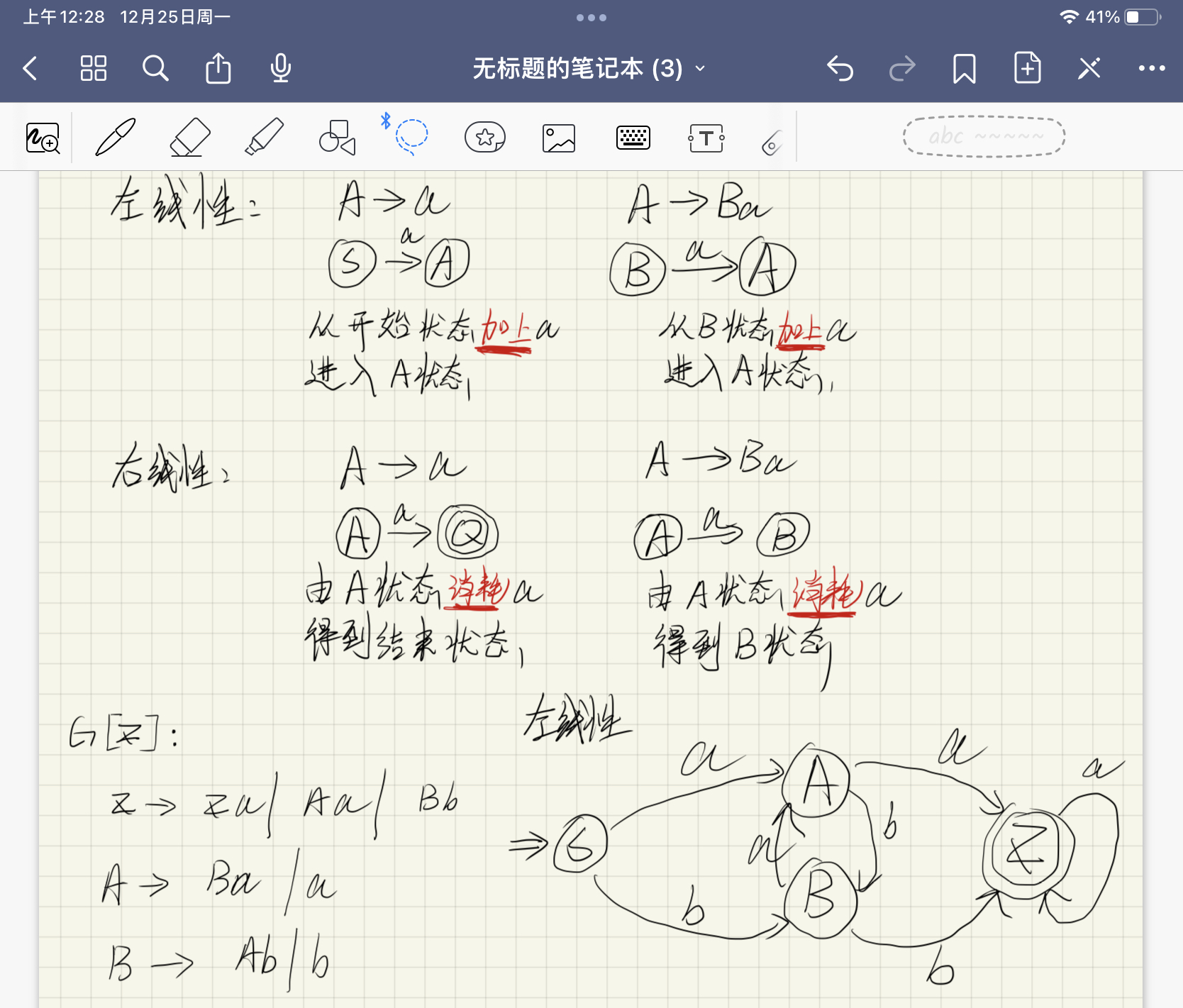
- 0型文法(1型文法) : 上下文有关文法,(产生式的左部参杂着终结符)
- 2型文法 : 上下文无关文法,(产生式的左部只有非终结符)
- 3型文法 : 正规文法
- 每个规则只能具有下面两种形式,并且正规文法中只能出现其中一种
- 第一种(终结符+非终结符)
A::=aA::=aB(右线性文法)
- 第二种(非终结符+终结符)
A::=aA::=Ba(左线性文法)
- 第一种(终结符+非终结符)
- 每个规则只能具有下面两种形式,并且正规文法中只能出现其中一种
语法分析树(推导树)
- 语法树上的每一个节点都是终结符或非终结符
- 树根是文法的开始符
- 分支,
- 有分支的一定是非终结符,
- 没有分支的,无法判定
- 一个节点有分支,一定能找到一条规则
- B节点有两个子节点,则文法中一定有一条规则:
B->bd
- B节点有两个子节点,则文法中一定有一条规则:
- 子树:某节点的子树就是该节点及其向下的部分,
- 层数:比如下面的案例,S有3层,A有2层,B有1层。
- 简单子树:只含有单层分支的子树(层数为1的子树),如B
- 最左推导:每一步的推导总是替换掉最左边的非终结符
- 最右推导(规范推导):(反过来)
- 规约序列:
- 最左规约为规范规约。
- 从句子通过一次次规约,规约到文法开始符号,就可以证明该句子是该文法所定义的语言中的一个句子。
- 最左规约和最有推导互为逆过程
- 规范句型(右句型)
- 通过规范推导得出的句型都叫规范句型。
案例
G[S]:
S->aAB
A->Ba|a
B->bd
最左推导过程:
S => aAB => a(Ba|a)B => a((bd)a|a)B => a((bd)a|a)(bd)
最右推导过程(规范推导):
S => aAB => aA(bd) => a(Ba|a)((Ba|a)) => a((bd)a|a)(bd)
上面的 aAB aAbd 都是规范句型,最后一个是句子,但句子也是特殊的句型,所以最后一个也是规范句型。
最左规约(规范规约)序列:
abdabd =△> aBabd =△> aAbd =△> aAB =△> S
推导树:
S
|____
| | |
a A B
| |__
| | |
| b d
|__
| |
B a
|__
| |
b d二义性
- 如果一个文法存在某个句子对应两颗完全不同语法树,则说这个文法是二义性的,这个句子是二义性句子
- 或者说一个文法中只要有某个句子,他的左推导和右推导是不同的,则这个文法是二义性的文法,这个句子是二义性的句子
- 句型:一个句型可以有多课语法树,最左推导和最右推导可以不同
- 句子: 一个句子只能有一颗语法树,最左推导和最右推导必须相同,否则就是具有二义性
- 注意:文法的二义性和语言的二义性概念不同
- 如果一个语言的所有文法都是二义性文法,则称该语言是先天性二义性语言
这个文法就是二义性文法,因为左推导和右推导将推出完全不同的推导树。
G[E]: E -> E+E -> E*E -> (E) | i
左推导:E => E+E => E*E+E => i*i+i
右推导:E => E+E => E+E*E => i+i*i
由于之前写过编译器和解释器,这里尝试着消除二义性:
G[AddExpression]:
AddExpression
:= MutExpression
| AddExpression + MutExpression
;
MutExpression
:= FactorExpression
| MutExpression * FactorExpression
;
FactorExpression
:= BracketedExpression
| i
;
BracketedExpression
:= ( AddExpression )
;句型的分析
- 语法树是句型推导的几何表示(上下文无关文法)
- 语法树是句型分析的好工具
- 句型分析就是识别符号串是否为某文法的句型
- 这也是为什么语法树也被叫做分析树、语法分析树
- 完成句型分析的程序成为分析程序、识别程序
- 分析算法又称为识别算法
分析算法
- 从左到右的分析算法
- 自顶向下分析法
- 从文法的开始符号出发,反复用各种产生式,寻找和输入字符串匹配的推导。
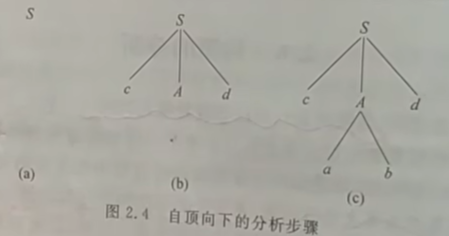
- 自底向上分析法
- 从输入符号串开始,逐步进行规约,直至规约到文法的开始符号
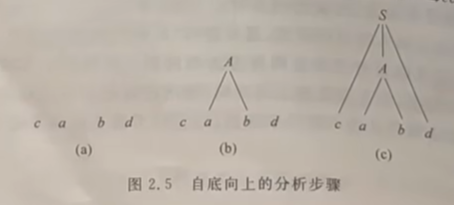
- 自顶向下分析法
- 从右到左的分析算法
自底向上分析法
- 短语:在一个子树中,末端节点是子树树根的短语。
- 简单短语(直接短语):在一个简单子树中,由末端节点所组成的符号串就是简单子树树根的简单短语。
- 句柄:最左简单子树的末端节点组成的符号串是句柄。
- 句柄只适用于规范句型,规范句型只在规范推导中出现,
- 规范推导就是最右推导,最右推导又对应着最左规约。
G[S]:
S->aAB
A->Ba|a
B->bd
最左推导过程:
S => aAB => a(Ba|a)B => a((bd)a|a)B => a((bd)a|a)(bd) => abdabd | aabd
推导树:
S
|____
| | |
a A B
| |__
| | |
| b d
|__
| |
B a
|__
| |
b d
求句型abdabd的短语、简单短语、句柄。
短语
abdabd是该句型相对于S的短语
bda是该句型相对于A的短语
bd是该句型相对于B的短语
简单短语(找出短语之后,找出哪些只有一层的子树):
bd是该句型相对于B的简单短语
句柄(找出所有简单短语中最左边的):
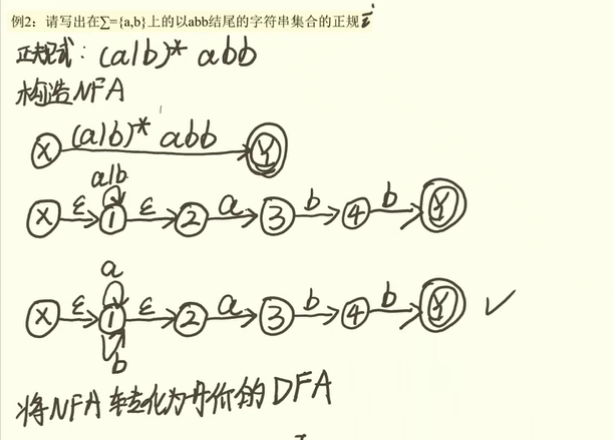
bd正规式和有穷自动机
- 正规式:将符号表
Σ上的字母用*.|连接组成的表达式()括号的优先级最高, 然后依次为:*字符的闭包运算,.字符的乘积运算,这个符号有时候可以省略|字符的加法运算,读作或,也可以写成+
- 正规集:由正规式所描述的符号串所组成的集合
- 正规式与正规集的案例
正规式描述标识符:
(a|b|c|....|z)(a|..|z|0|...0)*
文法描述:
G[<标识符>]:
<标识符> -> <字母>
<标识符> -> <标识符><数字>
<字母> -> a|b|c|...|z
<数字> -> 0|1|2|...|9DFA的构造
- 乘积运算可以在状态图的中间加一个状态来实现
- 或运算可以用两条箭头来实现
- 闭包运算是一个自循环,前后两个空字符串
- 开始状态一个圈,结束状态两个圈
根据文法构建状态机
五元组定义DFA
D_1 = (
状态的集合K,
状态机可接受的终结符Σ,
转换函数M,
有穷状态机初态S,
终止状态的集合F
)
K = {S,A,B,Z}
Σ = {a,b}
M:
M(S,a)=A M(S,b)=B
M(A,a)=Z M(A,b)=B
M(B,b)=Z M(B,a)=A
M(Z,a)=Z
S = S
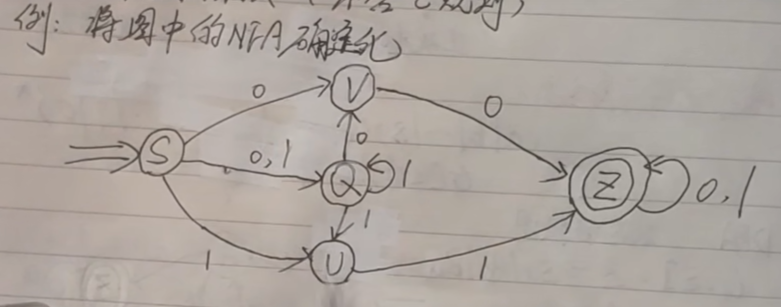
F = {Z}NFA的确定化
- NFA:不确定的有穷自动机
- DFA: 确定的有穷自动机
- 方法:
- 子集法(可处理
ε规则) - 简化的子集法(不能处理ε规则)
- 子集法(可处理
例题
解
- 先画出其状态转换表
| K\Σ | 0 | 1 |
|---|---|---|
| S | V,Q | Q,U |
| V | Z | |
| Q | V | Q,U |
| U | Z | |
| Z | Z | Z |
- 然后构造新的等价的
DFA(K',Σ,M',S',F') - 这张表中就包含了
K'和M'
K'\ Σ | 0 | 1 |
|---|---|---|
| [S] | [V,Q] | [Q,U] |
| [V,Q] | [V,Z] | [Q,U] |
| [Q,U] | [V] | [Q,U,Z] |
| [V,Z] | [Z] | [Z] |
| [Q,U,Z] | [V,Z] | [Q,U,Z] |
| [V] | [Z] | |
| [Q] | [V] | [Q,U] |
| [U] | [Z] | |
| [Z] | [Z] | [Z] |
S' = [S]
新的开始状态F' = { [V,Z] , [Q,U,Z] , [Z] }- 新的终止状态状态,是所有状态中,包含旧的终止状态的集合
语法分析
自顶向下的语法分析
LL(1)文法
- 第一个L,表示从左向右扫描
- 第二个L,表示最左推导
- 1 表示向前看1个字符
首符号集First(α)
- 找到
α最左边可能出现的终结符 - 技巧,向左看

后跟符号集Follow(A)
- 表示的是非终结符A后面可以跟的所有终结符的集合(A属于V_N)
- 求解步骤
#∈Follow(S)S为识别符号- 意思是先把
#放入集合中 G[识别符号]:
- 意思是先把
- 若存在规则
T->XWY则First(y)-{ε}∈Follow(W)- Y可能是终结符也可能是非终结符
- 这里就是说,W的后跟符号集,一定包含Y的首符号集减去空串。
- 若存在规则
T->XW或(T->XWY,其中Y =*=> ε),则Follow(T)∈Follow(W)- 就是说T的后更符号集一定也是W的后跟符号集
- 比如aTb,使用T—>XW规则,就变成了aXWb。这样,原来T后面的b自然就变成了W后面的了
- 技巧,向右看
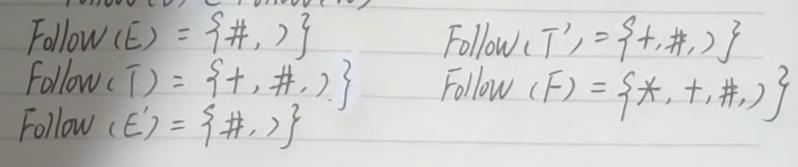
Follow(E) = {#} ∪ {)} = {#,)}
Follow(T) = (First(E')-{ε}) ∪ Follow(E') = {+,#,)}
Follow(E') = Follow(E) = {#,)}
Follow(T') = Follow(T) = {+,#,)}
Follow(F) = (First(T')-{ε}) ∪ Follow(T) ∪ Follow(T') = {*,+,#,)}选择符号集合:SELECT(A->α)
如果
α不能广义推导出ε则SELECT(A->α) = First(α)如果
α能广义推导出ε则(SELECT(A->α)-{ε}) ∪ Follow(A)
LL(1)文法
- 自顶向下的分析技术
- 对于每个非终极符A的任意两个产生式
A->α A->β - 满足:
Select(A->α) ∩ Select(A->β) = ∅α和β至多只能有一个能推导出ε
- 判定:
- 含相同左部的产生式的可选集交集均为空集,则该文法是LL(1)文法。
- 其实说的就是上面的表达式。
- 就是去看它的文法定义,找出所有左部相同的产生式,然后证明:
Select(A->B) ∩ Select(A->B) ∩ Select(A->C) = ∅
- 含相同左部的产生式的可选集交集均为空集,则该文法是LL(1)文法。
将非LL(1)文法等价变化为LL(1)文法
- 提取左公因子
- 消除左递归
- 消除间接左递归
- 略
- 消除文法中的一切左递归
- 略
LL(1)文法分析的实现
- 递归下降法
- 表驱动