跳至主要內容

蓝桥杯 2013 年 java B 组真题刷题笔记

丁毅桂大约 23 分钟算法蓝桥杯JAVA算法刷题笔记

蓝桥杯 2013 年 java B 组真题刷题笔记

目录

[01]世纪末的星期

曾有邪教称 1999 年 12 月 31 日是世界末日。

当然该谣言已经不玫自破，还有人称今后的某个世纪末的 12 月 31 日，如果是星期一则会....

有趣的是，任何一个世纪末的年份的 12 月 31 日都不可能是星期—，于是，“谣言制造商"”又修改为星期日......

1999 年的 12 月 31 日是星期五，请问:未来哪一个离我们最近的一个世纪未年（即 xx99 年)的 12 月 31 日正好是星期天〈即星期日)?

请回答该年份(只写这个 4 位整数，不要写 12 月 31 等多余信息)

注意

  • 1970 年之前的日期无法用 calendarAPI
  • 要注意题目给的 1999 年的 12 月 31 日是星期五 是否和现实一致。否则可能是要假设这一天是星期五，然后向后推算，要考虑闰年和余年
package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.util.Calendar;

public class _01_世纪末的星期 {
 static void doSomeThing() {
  Calendar calendar = Calendar.getInstance();
  for (int year = 1999; year <= 9999; year += 100) {// 每次增加100年
   calendar.set(Calendar.YEAR, year);
   calendar.set(Calendar.MONTH, 11);// 1月是0 12月是11
   calendar.set(Calendar.DAY_OF_MONTH, 31);// 1号是1

   int dayOfWeek = calendar.get(Calendar.DAY_OF_WEEK);
   System.out.println("year:" + year + " week:" + dayOfWeek);
   if (dayOfWeek == Calendar.SUNDAY) {
    break;
   }
  }
 }

 public static void main(String[] args) {
  long start = System.currentTimeMillis();
  doSomeThing();
  long end = System.currentTimeMillis();
  System.out.println("耗时:" + (end - start) + "毫秒");
  /*
   * year:1999 week:6 # 6是星期五
   * year:2099 week:5
   * year:2199 week:3
   * year:2299 week:1 # 1是星期日
   * 耗时:37毫秒
   */
 }
}

[02]马虎的算式

标题: 马虎的算式

小明是个急性子，上小学的时候经常把老师写在黑板上的题目抄错了。

有一次，老师出的题目是：36 x 495 = ?

他却给抄成了：396 x 45 = ?

但结果却很戏剧性，他的答案竟然是对的！！

因为 36 * 495 = 396 * 45 = 17820

类似这样的巧合情况可能还有很多，比如：27 * 594 = 297 * 54

假设 a b c d e 代表1~9不同的5个数字（注意是各不相同的数字，且不含0）

能满足形如： ab * cde = adb * ce 这样的算式一共有多少种呢？

请你利用计算机的优势寻找所有的可能，并回答不同算式的种类数。

满足乘法交换律的算式计为不同的种类，所以答案肯定是个偶数。

答案直接通过浏览器提交。
注意：只提交一个表示最终统计种类数的数字，不要提交解答过程或其它多余的内容。

思路：直接暴力枚举尝试所有的可能。

要注意如何防止重复，集合去重的写法不需要脑子，if 去重的写法要掌握规律

集合去重的写法

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.util.HashSet;
import java.util.Set;

public class _02_马虎的算式 {
 public static void main(String[] args) {

  int count = 0;
  for (int a = 1; a <= 9; a++) {
   for (int b = 1; b <= 9; b++)
    for (int c = 1; c <= 9; c++)
     for (int d = 1; d <= 9; d++)
      for (int e = 1; e <= 9; e++) {
       Set<Integer> set = new HashSet<Integer>();
       set.add(a);
       set.add(b);
       set.add(c);
       set.add(d);
       set.add(e);
       if (set.size() != 5)// 去除重复
        continue;

       // ab*cde == adb*ce;
       if ((a * 10 + b) * (c * 100 + d * 10 + e) == (a * 100 + d * 10 + b) * (c * 10 + e)) {
        System.out.println("" + a + b + "*" + c + d + e + "==" + a + d + b + "*" + c + e);
        count++;
       }
      }
  }
  System.out.println("total:" + count);
  /*
   * 输出:
   * ......略
   * 81*495==891*45
   * 81*594==891*54
   * 81*693==891*63
   * 81*792==891*72
   * 84*596==894*56
   * 91*532==931*52
   * 96*234==936*24
   * 98*134==938*14
   * 98*536==938*56
   * total:142
   */
 }
}

if 去重的写法

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

public class _02_马虎的算式 {
 public static void main(String[] args) {
  int count = 0;
  for (int a = 1; a <= 9; a++) {
   for (int b = 1; b <= 9; b++)
    if (b != a)
    for (int c = 1; c <= 9; c++)
     if (c != a && c != b)
     for (int d = 1; d <= 9; d++)
      if (d != a && d != b && d != c)
      for (int e = 1; e <= 9; e++) {
       if (e != a && e != b && e != c && e != d) {
        // ab*cde == adb*ce;
        if ((a * 10 + b) * (c * 100 + d * 10 + e) == (a * 100 + d * 10 + b)* (c * 10 + e)) {
         System.out.println("" + a + b + "*" + c + d + e + "==" + a + d + b + "*"+ c+ e);
         count++;
        }
       }
      }
  }
  System.out.println("total:" + count);
  /*
   * 输出:
   * ......略
   * 81*495==891*45
   * 81*594==891*54
   * 81*693==891*63
   * 81*792==891*72
   * 84*596==894*56
   * 91*532==931*52
   * 96*234==936*24
   * 98*134==938*14
   * 98*536==938*56
   * total:142
   */
 }
}

[03]振兴中华

标题:振兴中华

小明参加了学校的趣味运动会，其中的一个项目是:跳格子。

地上画着一些格子，每个格子里写一个字，如下所示:(也可参见 p1.jpg)

从我做起振
我做起撮兴
做起振兴中
起振兴中华

比赛时，先站在左上角的写着“从"字的格子里，
可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。
一直要跳到“华""字结裘
要求跳过的路线刚好构成"从我做起振兴中华"这句话。

请你帮助小明算一算他一共有多少种可能的跳跃路线呢?|

答案是一个整数，请通过浏览器直接提交该数字。

注意:不要提交解答过程，或其它辅助说明类的内容。

思路，动态规划问题。

记忆性递归解法

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

public class _03_振兴中华 {

 public static void main(String[] args) {
  long start = System.currentTimeMillis();
  doSomeThing();
  long end = System.currentTimeMillis();
  System.out.println("耗时:" + (end - start) + "毫秒");
 }

 /*
  * 从我做起振
  * 我做起振兴
  * 做起振兴中
  * 起振兴中华
  */
 static void doSomeThing() {
  System.out.println(process(0,0));
    // 35
        // 耗时:0毫秒
 }

 // 记忆性递归
 static int f[][] = new int[4][5];
 static int process(int x, int y) {
  if (x == 3 || y == 4) {
   return f[x][y] = 1;
  } else if (f[x][y] != 0) {
   return f[x][y];
  } else {
   return f[x][y] = process(x + 1, y) + process(x, y + 1);
  }
 }
}

暴力递归解法

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

public class _02_振兴中华 {

 public static void main(String[] args) {
  long start = System.currentTimeMillis();
  doSomeThing();
  long end = System.currentTimeMillis();
  System.out.println("耗时:" + (end - start) + "毫秒");
 }

 /*
  * 从我做起振
  * 我做起振兴
  * 做起振兴中
  * 起振兴中华
  */
 static void doSomeThing() {
  System.out.println(process(1, 1));
  // 35
        // 耗时:0毫秒
 }

 static int process(int x, int y) {
  if (x == 4 || y == 5)
   return 1;
  return process(x + 1, y) // 往下走一步
    + process(x, y + 1);// 往右走一步
 }

}

[04]黄金连分数

标题: 黄金连分数
    黄金分割数0.61803... 是个无理数，这个常数十分重要，在许多工程问题中会出现。有时需要把这个数字求得很精确。

    对于某些精密工程，常数的精度很重要。也许你听说过哈勃太空望远镜，它首次升空后就发现了一处人工加工错误，对那样一      个庞然大物，其实只是镜面加工时有比头发丝还细许多倍的一处错误而已，却使它成了“近视眼”!!
    言归正传，我们如何求得黄金分割数的尽可能精确的值呢？有许多方法。

    比较简单的一种是用连分数：

                  1
    黄金数 = ---------------------
                        1
             1 + -----------------
                          1
                 1 + -------------
                            1
                     1 + ---------
                          1 + ...

    这个连分数计算的“层数”越多，它的值越接近黄金分割数。

    请你利用这一特性，求出黄金分割数的足够精确值，要求四舍五入到小数点后100位。

    小数点后3位的值为：0.618
    小数点后4位的值为：0.6180
    小数点后5位的值为：0.61803
    小数点后7位的值为：0.6180340
   （注意尾部的0，不能忽略）

你的任务是：写出精确到小数点后100位精度的黄金分割值。

注意：尾数的四舍五入！ 尾数是0也要保留！

显然答案是一个小数，其小数点后有100位数字，请通过浏览器直接提交该数字。
注意：不要提交解答过程，或其它辅助说明类的内容。

思路

题目的意思是：\text{题目的意思是：}

黄金分割=11+(111+(111+(1...))) \text{黄金分割}=\frac{1}{1+(\frac{1}{\frac{1}{1+(\frac{1}{\frac{1}{1+(\frac{1}{...})}})}})}

从1开始算：\text{从1开始算：}

11+1=12 \frac{1}{1+1}=\frac{1}{2}

11+12=23 \frac{1}{1+\frac{1}{2}}=\frac{2}{3}

11+23=35 \frac{1}{1+\frac{2}{3}}=\frac{3}{5}

11+35=58 \frac{1}{1+\frac{3}{5}}=\frac{5}{8}

11+58=813 \frac{1}{1+\frac{5}{8}}=\frac{8}{13}

...... ......

最终发现分子分母是斐波那契数列：\text{最终发现分子分母是斐波那契数列：}

1,2,3,5,8,13,... 1,2,3,5,8,13,...

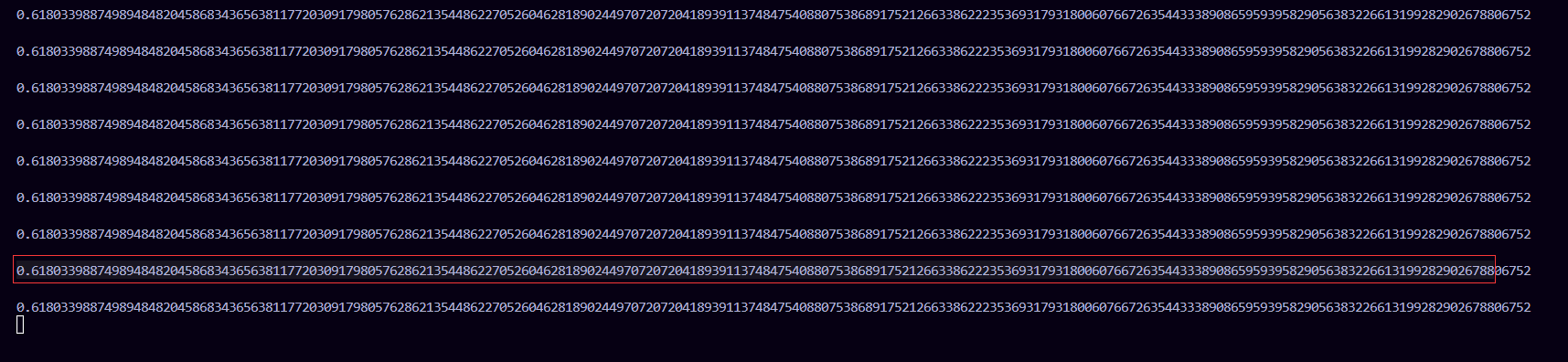
程序输出结果

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.math.BigDecimal;
import java.math.RoundingMode;
import java.util.Iterator;
import java.util.Scanner;

public class _04_黄金连分数 {
 // 黄金分割数生成器
 static class GoldNumber implements Iterator {
  BigDecimal a;
  BigDecimal b;
  BigDecimal c;
  GoldNumber() {
   a = BigDecimal.valueOf(1);
   b = BigDecimal.valueOf(2);
   c = a.add(b);
  }
  @Override
  public boolean hasNext() {
   return true;
  }
  @Override
  public Object next() {
   BigDecimal next = a.divide(b, 220, RoundingMode.HALF_DOWN);// 不要四舍五入
   a = b;
   b = c;
   c = a.add(b);
   return next;
  }
 }

 public static void main(String[] args) {
  Scanner sc = new Scanner(System.in);
  GoldNumber gd = new GoldNumber();
  String res;
  while (true) {
   BigDecimal bd = (BigDecimal) gd.next();
   res = bd.toString();
   System.out.println(res.toString().substring(0, 2 + 200 + 5));// 保留小数点后205位
   sc.nextLine();
  }
  // 0.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748475408807538689175212663386222353693179318006076672635443338908659593958290563832266131992829026788 06752
 }
}

[05]有理数类

有理数就是可以表示为两个整数的比值的数字。

-般情况下，我们哪似的小数表示。但有些时候，不允许出现误差，必须用两个整数来表示一个有理数。

这时，我们可以建立一个“有理数类”， 下面的代码初步实现了这个目标。为了简明，它只提供了加法和乘法运算。

题目：完成有理数类的加法运算

 class Rational {
  private long ra;
  private long rb;

  // 求最大公因数
  private long gcd(long a, long b) {
   if (b == 0)
    return a;
   return gcd(b, a % b);
  }

  public Rational(long a, long b) {
   ra = a;
   rb = b;

   long k = gcd(ra, rb);// 求最大公因数
   if (k > 1) {
    ra /= k;// 约分化简
    rb /= k;
   }
  }

  // 加法
  public Rational add(Rational x) {
   // 需要补充完整的部分
   return null;
  }

  // 乘法
  public Rational mul(Rational x) {
   return new Rational(ra * x.ra, rb * x.rb);
  }

  @Override
  public String toString() {
   if (rb == 1)
    return ra + "";
   else
    return ra + "/" + rb;
  }
 }

1/2+5/6=4/3
耗时:1毫秒

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

public class _05_有理数类 {

 static void doSomeThing() {
  Rational a = new Rational(2, 4);
  Rational b = new Rational(5, 6);
  Rational c = a.add(b);
  System.out.println(a + "+" + b + "=" + c);
  // 1/2+5/6=4/3
  // 耗时:1毫秒
 }

 public static void main(String[] args) {
  long start = System.currentTimeMillis();
  doSomeThing();
  long end = System.currentTimeMillis();
  System.out.println("耗时:" + (end - start) + "毫秒");
 }

 // 用分数表示的有理数
 static class Rational {
  private long ra;// 分子
  private long rb;// 分母
  public Rational(long a, long b) {
   ra = a;
   rb = b;
   long k = gcd(ra, rb);// 求最大公因数/最大公约数
   if (k > 1) {
    ra /= k;// 约分化简
    rb /= k;
   }
  }
  // 求最大公因数/最大公约数
  private long gcd(long a, long b) {
   if (b == 0)
    return a;
   return gcd(b, a % b);
  }
  // 加法
  public Rational add(Rational x) {
   return new Rational(
    this.ra * x.rb + x.ra * this.rb,
    this.rb * x.rb
   );
  }
  // 乘法
  public Rational mul(Rational x) {
   return new Rational(ra * x.ra, rb * x.rb);
  }
  @Override
  public String toString() {
   if (rb == 1)
    return ra + "";
   else
    return ra + "/" + rb;
  }
 }
}

[06]三部排序

标题:三部推序

-般的排序有许多经典算法，如快速排序、希尔排序等。

但实际应用时，经常会或多或少有一些特殊的要求。 我们没必要套用那些经典算法，可以根据实际情况建立更好的解法。

比如，对-个整型数组中的数字进行分类排序:

使得负数都靠左端，正数都靠右端， 在中部。注意问题的特点是:负数区城和正数区域内并不要求有序。可以利用这个特点通过 1 次线性扫描就结束战斗!!

以下的程序实现了该目标。

 static void sort(int[] x) {
  int p = 0;
  int left = 0;
  int right = x.length - 1;
  while (p <= right) {
   if (x[p] < 0) {
    int t = x[left];
    x[left] = x[p];
    x[p] = t;
    left++;
    p++;
   } else if (x[p] > 0) {
    int t = x[right];
    x[right] = x[p];
    x[p] = t;
    right--;
   } else {
    // _____; //代码填空位置
   }
  }
 }

思路
实际上就是荷兰国旗问题。
或者说就是快速排序中的分治法

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.util.Arrays;

public class _06_三部排序 {
 static void sort(int[] x) {
  int p = 0;
  int left = 0;
  int right = x.length - 1;
  while (p <= right) {
   if (x[p] < 0) {
    int t = x[left];
    x[left] = x[p];// x[left]是小于0的数区间的下一个数
    x[p] = t;// x[p]是小于0的数
    left++;
    p++;// p要向后挪，
   } else if (x[p] > 0) {
    int t = x[right];//x[right]是大于0的数的区间的前一个数
    x[right] = x[p];
    x[p] = t;
    right--;
    // p不要向后挪动，因为要判断交换后的这个数应该怎么放
   } else {
    p++;// 此处就是x[p]==0的情况，直接跳过即可
   }
  }
 }
 public static void main(String[] args) {
  int arr[] = new int[]{-1,0,3,-4,0,6,7,-8,0,10};
  sort(arr);
  System.out.println(Arrays.toString(arr));
  // [-1, -4, -8, 0, 0, 0, 7, 6, 10, 3]
 }
}

[07]错误票据

题目：
某涉密单位下发了某种票据，并要在年终全部收回。

每张票据有唯一的ID号。全年所有票据的ID号是连续的，但ID的开始数码是随机选定的。

因为工作人员疏忽，在录入ID号的时候发生了一处错误，造成了某个ID断号，另外一个ID重号。

你的任务是通过编程，找出断号的ID和重号的ID。

假设断号不可能发生在最大和最小号。

输入格式

要求程序首先输入一个整数N(N<100)表示后面数据行数。

接着读入N行数据。

每行数据长度不等，是用空格分开的若干个（不大于100个）正整数（不大于100000），请注意行内和行末可能有多余的空格，你的程序需要能处理这些空格。

每个整数代表一个ID号。

输出格式

要求程序输出1行，含两个整数m n，用空格分隔。

其中，m表示断号ID，n表示重号ID

样例输入1

2
5 6 8 11 9
10 12 9

样例输出1

7 9
///
样例输入2

6
164 178 108 109 180 155 141 159 104 182 179 118 137 184 115 124 125 129 168 196
172 189 127 107 112 192 103 131 133 169 158
128 102 110 148 139 157 140 195 197
185 152 135 106 123 173 122 136 174 191 145 116 151 143 175 120 161 134 162 190
149 138 142 146 199 126 165 156 153 193 144 166 170 121 171 132 101 194 187 188
113 130 176 154 177 120 117 150 114 183 186 181 100 163 160 167 147 198 111 119

样例输出2

105 120

package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Scanner;

public class _07_错误票据 {
 static Map<Integer, Integer> map = new HashMap<>();

 static List<Integer> list = new ArrayList<>();

 public static void main(String[] args) {

  Scanner sc = new Scanner(System.in);
  int n = sc.nextInt();
  sc.nextLine();// 读完这一行

  for (int i = 0; i < n; i++) {
   String line = sc.nextLine();// 直接读入一行
   String nums[] = line.split(" ");// 按空格分割
   for (String num : nums) {
    Integer id = Integer.valueOf(num);// 转换成数字
    list.add(id);
   }
  }
  Integer[] ids = new Integer[list.size()];
  list.toArray(ids);
  Arrays.sort(ids);
  Integer a = null, b = null;
  for (int i = 0; i < ids.length - 1; i++) {
   // 此处有坑， Integer 比较要用equals
   if (ids[i].equals( ids[i + 1])) {
    b = ids[i];// 当前的数和下一个数相同则重复
    continue;
   }
   if (ids[i + 1] != ids[i] + 1) {
    a = ids[i] + 1;// 当前的数+1 不等于 下一个数 则表面缺了一个
   }
  }
  System.out.println("缺失的数：" + a);
  System.out.println("重复的数：" + b);
  // 6
        // 164 178 108 109 180 155 141 159 104 182 179 118 137 184 115 124 125 129 168 196
        // 172 189 127 107 112 192 103 131 133 169 158
        // 128 102 110 148 139 157 140 195 197
        // 185 152 135 106 123 173 122 136 174 191 145 116 151 143 175 120 161 134 162 190
        // 149 138 142 146 199 126 165 156 153 193 144 166 170 121 171 132 101 194 187 188
        // 113 130 176 154 177 120 117 150 114 183 186 181 100 163 160 167 147 198 111 119
        // 缺失的数：105
        // 重复的数：120
 }
}

[08]幸运数

际题 ∶ 幸运数

幸运数是波兰数学家乌拉姆命名的。它采用与生成素数类似的“筛法"生成。
首先从 1 开始写出自然歌 1,2,3,4,5,6,. . ..

1 就是第—个幸运数。

我们从 2 这个数开始。把所有序号能被 2 整除的项删除，变为:
1 3 5 7 9 ....

把它们缩紧，重新记序，为:

1 3 5 7 9 ....。

这时，3 为第 2 个幸运数，然后把所有能被 3 整除的序号位置的数删去。

注意，是序号位置，不是那个数本身能否被 3 整除!!删除的应该是 5，11，17，...

此时 7 为第 3 个幸运数，然后再删去序号位置能被 7 整除的(19,39,.. .)

最后剩下的序列类似︰

1，3，7，9，13，15，21，25，31，33，37，43，49，51，63，67，69，73，75，79，...

本题要求:

输入两个正整敌 m n，用空格分开(m< n < 1000*1000)曝序输出位于 m 和 n 之问的幸运数的个数(不包含 m 和 n)。

生成幸运数的思路

  • 先生成 0-n 的自然数
  • 然后生成幸运数：
    • 挑选第 k=2 个数，m=arr[k]
    • 将数组中第 k 个及之后的所有数，若其下标是 m 的因数，则删除所有这些数
      • 删除的具体方法是：
      • 先遍历所有的数，将要删除的数标记为-1，表示删除。
      • 然后重新遍历所有数，做原地填充数组的操作，
      • 原地填充的具体步骤是,
      • 遍历，从第 i=1 开始，若找到一个数是不需要删除的，则放到 i 的位置，然后 i++
    • k++;
package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.util.Arrays;
import java.util.Scanner;

public class _08_幸运数 {
 static void doSomeThing() {
  Scanner sc = new Scanner(System.in);
  int m = 1;// sc.nextInt();
  int n = 20;// sc.nextInt();
  sc.close();
  int[] arr = new int[n + 1];

  for (int i = 1; i < arr.length; i++) {
   // 在1~n的位置生成1~n的自然数
   arr[i] = i;// 因为幸运数中的下标概念是从1开始算的，所以从1开始
  }

  System.out.println("生成自然数: " + Arrays.toString(arr));

  for (int idx = 2; // 从2开始
    idx < arr.length && arr[idx] != -1; // 提前结束
    idx++) {
   // 根据数组中第i位的数来删除
   deleteByN(arr, idx, arr[idx]);
  }

  System.out.println("生成幸运数: " + Arrays.toString(arr));

  // 输出这些数
  StringBuilder sb = new StringBuilder();
  for (int idx = 1; // 从1开始
    idx < arr.length && arr[idx] != -1; // 提前结束
    idx++) {
   // 找出m和n之间的数
   if (m < arr[idx] && arr[idx] < n) {
    sb.append(arr[idx]);
    sb.append(',');
   }
  }
  sb.deleteCharAt(sb.length() - 1);// 删除最后一个多余的逗号
  System.out.println("m:" + m + ",n:" + n);
  System.out.println("m n之间的幸运数是: " + sb.toString());

  // 输出这些数有多少个
  Integer startIndex = null;
  Integer endIndex = 1;
  for (int idx = 1; // 从1开始
    idx < arr.length && arr[idx] != -1; // 提前结束
    idx++) {

   if (startIndex == null && m < arr[idx]) {
    startIndex = idx;
   }
   if (arr[idx] < n) {
    endIndex = idx;
   } else {
    break;
   }
  }
  System.out.println("这些数的个数: " + (endIndex - startIndex));

 }

 // 删除位置下标是n倍数的数
 static void deleteByN(int[] arr, int startFrom, int n) {
  int next = startFrom;
  for (int idx = startFrom; // 从startFrom开始
    idx < arr.length && arr[idx] != -1; // 当等于-1时，后续的数都不再判断
    idx++) {
   if (idx % n == 0) {
    arr[idx] = -1; // 标记为-1 表示删除
   }
   if (arr[idx] != -1) {
    exchange(arr, next++, idx); // 将非-1的数往前挪动
   }
  }
 }

 static void exchange(int[] arr, int idxA, int idxB) {
  if (idxA != idxB) {
   arr[idxA] = arr[idxA] ^ arr[idxB];
   arr[idxB] = arr[idxA] ^ arr[idxB];
   arr[idxA] = arr[idxA] ^ arr[idxB];
  }
 }

 public static void main(String[] args) {
  long start = System.currentTimeMillis();
  doSomeThing();
  long end = System.currentTimeMillis();
  System.out.println("耗时:" + (end - start) + "毫秒");
 }
}

输出

生成自然数: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
生成幸运数: [0, 1, 3, 5, 7, 11, 13, 17, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1]
m:1,n:20
m n之间的幸运数是: 3,5,7,11,13,17
这些数的个数: 5

[09]带分数

思路

  • 先生成 1~9 的全排列
  • 再生成的全排列中提取数，
  • 假设其中一个全排列是[1,2,3,4,5,6,7,8,9]，则
  • 可提取 a=1 b=2 c=3456789
  • 可提取 a=1 b=23 c=456789
  • 可提取 a=1 b=234 c=56789
  • 然后判断是否 a+b/c==N即可
  • 可提取的数情况有很多种：
      • [1, 2, 3456789]
    • [1, 23, 456789]
    • [1, 234, 56789]
    • [1, 2345, 6789]
    • [1, 23456, 789]
    • [1, 234567, 89]
    • [1, 2345678, 9]
    • [12, 3, 456789]
    • [12, 34, 56789]
    • [12, 345, 6789]
    • [12, 3456, 789]
    • [12, 34567, 89]
    • [12, 345678, 9]
    • [123, 4, 56789]
    • [123, 45, 6789]
    • [123, 456, 789]
    • [123, 4567, 89]
    • [123, 45678, 9]
    • [1234, 5, 6789]
    • [1234, 56, 789]
    • [1234, 567, 89]
    • [1234, 5678, 9]
    • [12345, 6, 789]
    • [12345, 67, 89]
    • [12345, 678, 9]
    • [123456, 7, 89]
    • [123456, 78, 9]
    • [1234567, 8, 9]
package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.util.Arrays;
import java.util.Scanner;

public class _09_带分数 {
 private static int N = 0;
 static int counter = 0;

 public static void main(String[] args) {
  Scanner sc = new Scanner(System.in);
  N = sc.nextInt();

  long l1 = System.currentTimeMillis();
  f(nums, 0);
  long l2 = System.currentTimeMillis();

  System.out.printf("共%d种.\n", counter);
  System.out.printf("耗时:%dms\n", l2 - l1);
 }

 static int[] nums = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };

 // 全排列
 static void f(int[] array, int step) {
  if (step == array.length) {
   // 得到全排列的结果
   // System.out.println(Arrays.toString(array));
   check(array);
   return;
  } else {
   for (int i = step; i < array.length; i++) {
    exchange(array, step, i);// 从后面的可选项中挑选一个放到当前位置
    f(array, step + 1);// 递归确认下一个位置的元素
    exchange(array, step, i);// 交换回来，恢复原样，回溯。
   }
  }
 }

 static void check(int[] arr) {

  // 每个数的长度都在[1,len-2]范围上，
  // 因为格式是 num1+num2/num3 每个数都至少占一位，也要至少给另外两个数预留一位
  for (int n1_len = 1; n1_len <= arr.length - 2; n1_len++) {
   /*
    * 此处可以优化,但为了代码好理解，这里保持原样
    * int n1 = parseInt(arr, 0, n1_len); if(n1>N) continue;
    */
   for (int n2_len = 1; n2_len <= arr.length - 2; n2_len++) {
    // n2_len的结束条件可以优化成 n2_len <= arr.length - n1_len - 1 即至少给n3预留一个位置
    for (int n3_len = 1; n3_len <= arr.length - 2; n3_len++) {
     // 其实n3的长度可以直接计算出来： n3_len = arr.length - n1_len - n2_len
     if (n1_len + n2_len + n3_len == arr.length) {// 长度合理
      // 提取出这些数
      int n1 = parseInt(arr, 0, n1_len);
      int n2 = parseInt(arr, 0 + n1_len, n2_len);
      int n3 = parseInt(arr, 0 + +n1_len + n2_len, n3_len);
      // System.out.println(Arrays.toString(arr));
      // System.out.println(n1);
      // System.out.println(n2);
      // System.out.println(n3);
      if (n2 % n3 == 0 && n1 + n2 / n3 == N) {
       System.out.printf("%d+%d/%d==%d\n", n1, n2, n3, N);
       counter++;
      }
     }
    }
   }
  }
 }

 static void exchange(int[] arr, int i, int j) {
  if (i != j) {
   arr[i] = arr[i] ^ arr[j];
   arr[j] = arr[i] ^ arr[j];
   arr[i] = arr[i] ^ arr[j];
  }
 }

 static int parseInt(int[] arr, int start, int len) {
  int res = 0;
  for (int i = start; i < start + len; i++) {
   res *= 10;
   res += arr[i];
  }
  return res;
 }

 // check的另一种实现
 static int i = 0;
 // 从arr中选数，连续选出，至少选出1位数构成一个数，所有数都要被选出，一共构成K个数,放到nums[]中
 static void select(int[] arr, int rest_len, int current, int K, int[] nums) {
  // 最后一个数是剩余的全部数构成的数
  if (K == 1) {
   nums[i] = parseInt(arr, current, rest_len);
   System.out.println(Arrays.toString(nums));
   return;
  } else {
   for (int len = 1; len <= rest_len - (K - 1); len++) {
    nums[i] = parseInt(arr, current, len);
    i++;
    select(arr, rest_len - len, current + len, K - 1, nums);
    i--;// 回溯
   }
  }
 }
 /*
  * nums=[1,2,3,4,5,6,7,8,9]
  * select(nums, nums.length, 0, 3, new int[3]);
  * 输出结果：
  * [1, 2, 3456789]
  * [1, 23, 456789]
  * [1, 234, 56789]
  * [1, 2345, 6789]
  * [1, 23456, 789]
  * [1, 234567, 89]
  * [1, 2345678, 9]
  * [12, 3, 456789]
  * [12, 34, 56789]
  * [12, 345, 6789]
  * [12, 3456, 789]
  * [12, 34567, 89]
  * [12, 345678, 9]
  * [123, 4, 56789]
  * [123, 45, 6789]
  * [123, 456, 789]
  * [123, 4567, 89]
  * [123, 45678, 9]
  * [1234, 5, 6789]
  * [1234, 56, 789]
  * [1234, 567, 89]
  * [1234, 5678, 9]
  * [12345, 6, 789]
  * [12345, 67, 89]
  * [12345, 678, 9]
  * [123456, 7, 89]
  * [123456, 78, 9]
  * [1234567, 8, 9]
  */

}

输入输出结果

100
3+69258/714==100
82+3546/197==100
81+5643/297==100
81+7524/396==100
94+1578/263==100
96+2148/537==100
96+1428/357==100
96+1752/438==100
91+5742/638==100
91+5823/647==100
91+7524/836==100
共11种.
耗时:380ms

[10]连号区间数

题目
小明这些天一直在思考这样一个奇怪而有趣的问题：

在 1∼N 的某个排列中有多少个连号区间呢？

这里所说的连号区间的定义是：

如果区间 [L,R] 里的所有元素（即此排列的第 L 个到第 R 个元素）递增排序后能得到一个长度为 R−L+1 的“连续”数列，则称这个区间连号区间。


当 N 很小的时候，小明可以很快地算出答案，但是当 N 变大的时候，问题就不是那么简单了，现在小明需要你的帮助。

输入格式
第一行是一个正整数 N，表示排列的规模。

第二行是 N 个不同的数字 Pi，**表示这 N 个数字的某一排列。**

输出格式
输出一个整数，表示不同连号区间的数目。

数据范围

1≤N≤10000,
1≤Pi≤N

输入样例1：
4
3 2 4 1
输出样例1：
7

输入样例2：
5
3 4 2 5 1
输出样例2：
9

样例解释
第一个用例中，有 7 个连号区间分别是：[1,1],[1,2],[1,3],[1,4],[2,2],[3,3],[4,4]
第二个用例中，有 9 个连号区间分别是：[1,1],[1,2],[1,3],[1,4],[1,5],[2,2],[3,3],[4,4],[5,5]

思路

  • 主要先要看懂题，题目说的是有 1~N 的全排列，然后给你其中一个排列，意思就是，会有 N 个数，且这 N 个数是不重复，不缺少的，正好是 1~N 的数。
  • 然后从这个排列中，连续选出几个数，排序后，这几个数正好是连续的数。这称为连号区间。
  • 对于选数的问题，就是
    • 从第一个数开始选，选一个，选两个，选三个....
    • 从第二个数开始选，选一个，选两个，选三个....
    • 从第三个数开始选，选一个，选两个，选三个....
    • ...
  • 对于判断是否连续的问题，可以将该区间的数排序，然后看排序后区间的数是否连续的。
  • 也可以不排序，因为这些数是不会重复的，不会出现[2,3,3,5,6]这样的情况
  • 所以对于[2,3,4,5,6] 这样的连续的区间来说，
  • 有特征：6-2+1 == 5 即 max-min+1==length
  • 所以只需要找出该区间的最大值和最小值，不必管它是否有序，
  • 只需要判断是否满足特征，即可知道这个区间的数排序后是否为连续的数
package 蓝桥杯历年真题刷题笔记._2013_java_B_;

import java.util.Scanner;

public class _10_连号区间数 {
 static int count = 0;

 public static void main(String[] args) {
  Scanner sc = new Scanner(System.in);
  int N = sc.nextInt();
  int[] arr = new int[N + 1];
  for (int i = 1; i <= N; i++) {
   arr[i] = sc.nextInt();
  }
  sc.close();
  for (int L = 1; L <= N; L++) {
   int min = arr[L];
   int max = arr[L];
   for (int R = L; R <= N; R++) {
    if(arr[R]<min) min=arr[R];// 记录该区间最小值
    if(arr[R]>max) max=arr[R];// 记录该区间最大值

    if(R==L) count++;// 单独一个数构成连续区间
    else if(R-L+1==max-min+1) count++;
    // 因为arr是1~N的某个排列，所以不会有重复的数，即：不会出现这样的排序[3,4,4,6]
    // 所以对于像 [3,4,5,6]这样的连续的数,有特征：6-3+1=4 即max-min+1 == length
    // print(arr, L, R);
   }
  }
  System.out.println(count);
 }

 private static void print(int[] arr, int l, int r) {
  StringBuilder sb = new StringBuilder();
  sb.append('[');
  for (int i = l; i <= r; i++) {
   sb.append(arr[i]);
   sb.append(',');
  }
  sb.deleteCharAt(sb.length() - 1);
  sb.append(']');
  System.out.println(sb.toString());
 }

}
贡献者: YiguiDing
MIT Licensed | Copyright © 2019-present Yigui-Ding