
洛谷题单《能力全面提升综合题单》刷题笔记
2023/3/27大约 85 分钟
洛谷题单《能力全面提升综合题单》刷题笔记
目录
Part 1 入门阶段
Part 1.1 从零开始
- P1421 小玉买文具
- P1909 买铅笔
- P1089 津津的储蓄计划
- P1085 不高兴的津津
- P1035 级数求和
- P1980 计数问题
- P1014 Cantor表
- P1307 数字反转
小玉买文具
# 小玉买文具
## 题目描述
班主任给小玉一个任务,到文具店里买尽量多的签字笔。已知一只签字笔的价格是 $1$ 元 $9$ 角,而班主任给小玉的钱是 $a$ 元 $b$ 角,小玉想知道,她最多能买多少只签字笔呢。
## 输入格式
输入只有一行两个整数,分别表示 $a$ 和 $b$。
## 输出格式
输出一行一个整数,表示小玉最多能买多少只签字笔。
## 样例 #1
### 样例输入 #1
```
10 3
```
### 样例输出 #1
```
5
```
## 提示
#### 数据规模与约定
对于全部的测试点,保证 $0 \leq a \leq 10^4$,$0 \leq b \leq 9$。满分答案:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
int b = sc.nextInt();
int sum = a*10+b;
int pri = 19;
System.out.println(sum/pri);
}
}买铅笔
# [NOIP2016 普及组] 买铅笔
## 题目背景
NOIP2016 普及组 T1
## 题目描述
P 老师需要去商店买 $n$ 支铅笔作为小朋友们参加 NOIP 的礼物。她发现商店一共有 $3$ 种包装的铅笔,不同包装内的铅笔数量有可能不同,价格也有可能不同。为了公平起 见,P 老师决定只买同一种包装的铅笔。
商店不允许将铅笔的包装拆开,因此 P 老师可能需要购买超过 $n$ 支铅笔才够给小朋友们发礼物。
现在 P 老师想知道,在商店每种包装的数量都足够的情况下,要买够至少 $n$ 支铅笔最少需要花费多少钱。
## 输入格式
第一行包含一个正整数 $n$,表示需要的铅笔数量。
接下来三行,每行用 $2$ 个正整数描述一种包装的铅笔:其中第 $1$ 个整数表示这种包装内铅笔的数量,第 $2$ 个整数表示这种包装的价格。
保证所有的 $7$ 个数都是不超过 $10000$ 的正整数。
## 输出格式
$1$ 个整数,表示 P 老师最少需要花费的钱。
## 样例 #1
### 样例输入 #1
```
57
2 2
50 30
30 27
```
### 样例输出 #1
```
54
```
## 样例 #2
### 样例输入 #2
```
9998
128 233
128 2333
128 666
```
### 样例输出 #2
```
18407
```
## 样例 #3
### 样例输入 #3
```
9999
101 1111
1 9999
1111 9999
```
### 样例输出 #3
```
89991
```
## 提示
铅笔的三种包装分别是:
- $2$ 支装,价格为 $2$;
- $50$ 支装,价格为 $30$;
- $30$ 支装,价格为 $27$。
P老师需要购买至少 $57$ 支铅笔。
如果她选择购买第一种包装,那么她需要购买 $29$ 份,共计 $2 \times 29 = 58$ 支,需要花费的钱为 $2 \times 29 = 58$。
实际上,P 老师会选择购买第三种包装,这样需要买 $2$ 份。虽然最后买到的铅笔数量更多了,为 $30 \times 2 = 60$ 支,但花费却减少为 $27 \times 2 = 54$,比第一种少。
对于第二种包装,虽然每支铅笔的价格是最低的,但要够发必须买 $2$ 份,实际的花费达到了 $30 \times 2 = 60$,因此 P 老师也不会选择。
所以最后输出的答案是 $54$。
【数据范围】
保证所有的 $7$ 个数都是不超过 $10000$ 的正整数。
【子任务】
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:

上表中“整倍数”的意义为:若为 $K$,表示对应数据所需要的铅笔数量 $n$ —定是每种包装铅笔数量的整倍数(这意味着一定可以不用多买铅笔)。
于 2022 年 12 月 23 日新加 Hack 数据三组。满分答案:
// package _01_入门阶段._01_从零开始.P1909买铅笔;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();// 需要的铅笔数
int[][] data = new int[3][2];
for (int i = 0; i < data.length; i++) {
data[i][0] = sc.nextInt();// 该包装铅笔数量
data[i][1] = sc.nextInt();// 该包装铅笔价格
}
// 一共就三种选择,只能选一种,找出最便宜的一种即可
int price = Integer.MAX_VALUE;
for (int i = 0; i < data.length; i++) {
int val = (int)Math.ceil(/*向上取整*/n / (double) data[i][0])/* 数量 */ * data[i][1]/* 价格 */;
if(val<price)price=val;
}
System.out.println(price);
}
}津津的储蓄计划
# [NOIP2004 提高组] 津津的储蓄计划
## 题目描述
津津的零花钱一直都是自己管理。每个月的月初妈妈给津津 $300$ 元钱,津津会预算这个月的花销,并且总能做到实际花销和预算的相同。
为了让津津学习如何储蓄,妈妈提出,津津可以随时把整百的钱存在她那里,到了年末她会加上 $20\%$ 还给津津。因此津津制定了一个储蓄计划:每个月的月初,在得到妈妈给的零花钱后,如果她预计到这个月的月末手中还会有多于 $100$ 元或恰好 $100$ 元,她就会把整百的钱存在妈妈那里,剩余的钱留在自己手中。
例如 $11$月初津津手中还有 $83$ 元,妈妈给了津津 $300$ 元。津津预计$11$月的花销是 $180$ 元,那么她就会在妈妈那里存 $200$ 元,自己留下 $183$ 元。到了 $11$ 月月末,津津手中会剩下 $3$ 元钱。
津津发现这个储蓄计划的主要风险是,存在妈妈那里的钱在年末之前不能取出。有可能在某个月的月初,津津手中的钱加上这个月妈妈给的钱,不够这个月的原定预算。如果出现这种情况,津津将不得不在这个月省吃俭用,压缩预算。
现在请你根据 $2004$ 年 $1$ 月到 $12$ 月每个月津津的预算,判断会不会出现这种情况。如果不会,计算到 $2004$ 年年末,妈妈将津津平常存的钱加上 $20\%$ 还给津津之后,津津手中会有多少钱。
## 输入格式
$12$ 行数据,每行包含一个小于 $350$ 的非负整数,分别表示 $1$ 月到 $12$ 月津津的预算。
## 输出格式
一个整数。如果储蓄计划实施过程中出现某个月钱不够用的情况,输出 $-X$,$X$ 表示出现这种情况的第一个月;否则输出到 $2004$ 年年末津津手中会有多少钱。
注意,洛谷不需要进行文件输入输出,而是标准输入输出。
## 样例 #1
### 样例输入 #1
```
290
230
280
200
300
170
340
50
90
80
200
60
```
### 样例输出 #1
```
-7
```
## 样例 #2
### 样例输入 #2
```
290
230
280
200
300
170
330
50
90
80
200
60
```
### 样例输出 #2
```
1580
```满分答案:
package _01_入门阶段._01_从零开始.P1089津津的储蓄计划;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] expect = new int[12];// 每个月的预算
for (int i = 0; i < expect.length; i++) {
expect[i] = sc.nextInt();
}
int save = 0;
int rest = 0;
for (int i = 0; i < expect.length; i++) {
rest += 300;
if (rest - expect[i] >= 0/* 够用 */) {
rest -= expect[i];// 花钱
int k = rest / 100 * 100;// 计算要存的整百数
rest -= k;// 存钱
save += k;// 存钱
} else {
System.out.println(-(i + 1));// 钱不够用输出月数
return;
}
}
System.out.println(rest + save * 12 / 10/* x1.2 */);
}
}不高兴的津津
# [NOIP2004 普及组] 不高兴的津津
## 题目描述
津津上初中了。妈妈认为津津应该更加用功学习,所以津津除了上学之外,还要参加妈妈为她报名的各科复习班。另外每周妈妈还会送她去学习朗诵、舞蹈和钢琴。但是津津如果一天上课超过八个小时就会不高兴,而且上得越久就会越不高兴。假设津津不会因为其它事不高兴,并且她的不高兴不会持续到第二天。请你帮忙检查一下津津下周的日程安排,看看下周她会不会不高兴;如果会的话,哪天最不高兴。
## 输入格式
输入包括 $7$ 行数据,分别表示周一到周日的日程安排。每行包括两个小于 $10$ 的非负整数,用空格隔开,分别表示津津在学校上课的时间和妈妈安排她上课的时间。
## 输出格式
一个数字。如果不会不高兴则输出 $0$,如果会则输出最不高兴的是周几(用 $1, 2, 3, 4, 5, 6, 7$ 分别表示周一,周二,周三,周四,周五,周六,周日)。如果有两天或两天以上不高兴的程度相当,则输出时间最靠前的一天。
## 样例 #1
### 样例输入 #1
```
5 3
6 2
7 2
5 3
5 4
0 4
0 6
```
### 样例输出 #1
```
3
```
## 提示
NOIP2004 普及组第 1 题
- 2021-10-27:增加一组 hack 数据
- 2022-06-05:又增加一组 hack 数据满分答案:
package _01_入门阶段._01_从零开始.P1085不高兴的津津;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] data = new int[7];
for (int i = 0; i < data.length; i++) {
data[i] = sc.nextInt() + sc.nextInt();
}
int maxIdx = -1;
int maxVal = Integer.MIN_VALUE;
for (int i = 0; i < data.length; i++) {
if (data[i] > 8 && data[i] > maxVal) {
maxVal = data[i];
maxIdx = i;
}
}
maxIdx += 1;
System.out.println(maxIdx);
}
}级数求和
# [NOIP2002 普及组] 级数求和
## 题目描述
已知:$S_n= 1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$。显然对于任意一个整数 $k$,当 $n$ 足够大的时候,$S_n>k$。
现给出一个整数 $k$,要求计算出一个最小的 $n$,使得 $S_n>k$。
## 输入格式
一个正整数 $k$。
## 输出格式
一个正整数 $n$。
## 样例 #1
### 样例输入 #1
```
1
```
### 样例输出 #1
```
2
```
## 提示
**【数据范围】**
对于 $100\%$ 的数据,$1\le k \le 15$。
**【题目来源】**
NOIP 2002 普及组第一题满分答案:
package _01_入门阶段._01_从零开始.P1980级数求和;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int k = sc.nextInt();
int n = 0;
double s = 0;
while(s<k){
s+=1.0/++n;
}
System.out.println(n);
}
public static void main0(String[] args) {
// 错误尝试
// 不必使用有理数分式来计算,因为当k很大时,n也急剧增大,
// s的分子分母数组位数也极具增大,无法单纯用long表示,
// 应该仅在有理数**等值判断**时才使用有理分式。
Scanner sc = new Scanner(System.in);
Frac k = new Frac(sc.nextInt(), 1);
Frac s = new Frac(0, 1);
int n = 0;
while (s.compareTo(k) <= 0) {
s = s.add(new Frac(1, ++n));
System.out.println(s);
}
;
System.out.println(n);
}
}
/**
* Frac
*/
class Frac {
long a, b;
public Frac(long a, long b) {
this.a = a;
this.b = b;
long k = gcd(Math.abs(a), Math.abs(b));
this.a /= k;
this.b /= k;
}
Frac add(Frac other) {
return new Frac(this.a * other.b + other.a * this.b, this.b * other.b);
}
public long compareTo(Frac other) {
return this.a * other.b - other.a * this.b;
}
long gcd(long a, long b) {
return b == 0 ? a : gcd(b, a % b);
}
@Override
public String toString() {
return "Frac [" + a + "/" + b + "]";
}
}计数问题
# [NOIP2013 普及组] 计数问题
## 题目描述
试计算在区间 $1$ 到 $n$ 的所有整数中,数字 $x$($0\le x\le9$)共出现了多少次?例如,在 $1$ 到 $11$ 中,即在 $1,2,3,4,5,6,7,8,9,10,11$ 中,数字 $1$ 出现了 $4$ 次。
## 输入格式
$2$ 个整数 $n,x$,之间用一个空格隔开。
## 输出格式
$1$ 个整数,表示 $x$ 出现的次数。
## 样例 #1
### 样例输入 #1
```
11 1
```
### 样例输出 #1
```
4
```
## 提示
对于 $100\%$ 的数据,$1\le n\le 10^6$,$0\le x \le 9$。满分答案:
package _01_入门阶段._01_从零开始.P1980计数问题;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int x = sc.nextInt();
sc.close();
int[] cnt = new int[10];
for (int i = 1; i <= n; i++) {
int k = i;
while (k != 0) {
cnt[k % 10]++;
k /= 10;
}
}
System.out.println(cnt[x]);
}
}Cantor表
# [NOIP1999 普及组] Cantor 表
## 题目描述
现代数学的著名证明之一是 Georg Cantor 证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的:
$1/1$ , $1/2$ , $1/3$ , $1/4$, $1/5$, …
$2/1$, $2/2$ , $2/3$, $2/4$, …
$3/1$ , $3/2$, $3/3$, …
$4/1$, $4/2$, …
$5/1$, …
…
我们以 Z 字形给上表的每一项编号。第一项是 $1/1$,然后是 $1/2$,$2/1$,$3/1$,$2/2$,…
## 输入格式
整数$N$($1 \leq N \leq 10^7$)。
## 输出格式
表中的第 $N$ 项。
## 样例 #1
### 样例输入 #1
```
7
```
### 样例输出 #1
```
1/4
```满分答案:
package _01_入门阶段._01_从零开始.P1014Cantor表;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int n = 1;
int x = 1;
int y = 1;
int t = 1;
while (n < N) {
if (t % 2 == 0) {
y++;// 向下移动 ⬇
n++;
while (y != 1 && n < N) {
x += 1;// 对角线移动↗
y -= 1;
n++;
}
} else {
x++;// 向上移动 ↑
n++;
while (x != 1 && n < N) {
x -= 1;// 对角线移动↙
y += 1;
n++;
}
}
t++;
}
System.out.println(y + "/" + x);
}
}数字反转
# [NOIP2011 普及组] 数字反转
## 题目描述
给定一个整数 $N$,请将该数各个位上数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零(参见样例 2)。
## 输入格式
一个整数 $N$。
## 输出格式
一个整数,表示反转后的新数。
## 样例 #1
### 样例输入 #1
```
123
```
### 样例输出 #1
```
321
```
## 样例 #2
### 样例输入 #2
```
-380
```
### 样例输出 #2
```
-83
```
## 提示
**【数据范围】**
$-1,000,000,000\leq N\leq 1,000,000,000 $。
noip2011 普及组第一题满分答案:
package _01_入门阶段._01_从零开始.P1307数字反转;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
boolean sign = n < 0 ? true : false;
n = n < 0 ? -n : n;
StringBuilder sb = new StringBuilder();
sb.append((n + ""));
Integer k = Integer.valueOf(sb.reverse().toString());
k = sign ? -k : k;
System.out.println(k);
}
}Part 1.2 数组基础
- P1046 陶陶摘苹果
- P1047 校门外的树
- P1427 小鱼的数字游戏
- P2141 珠心算测验
- P5594 【XR-4】模拟赛
陶陶摘苹果
# [NOIP2005 普及组] 陶陶摘苹果
## 题目描述
陶陶家的院子里有一棵苹果树,每到秋天树上就会结出 $10$ 个苹果。苹果成熟的时候,陶陶就会跑去摘苹果。陶陶有个 $30$ 厘米高的板凳,当她不能直接用手摘到苹果的时候,就会踩到板凳上再试试。
现在已知 $10$ 个苹果到地面的高度,以及陶陶把手伸直的时候能够达到的最大高度,请帮陶陶算一下她能够摘到的苹果的数目。假设她碰到苹果,苹果就会掉下来。
## 输入格式
输入包括两行数据。第一行包含 $10$ 个 $100$ 到 $200$ 之间(包括 $100$ 和 $200$ )的整数(以厘米为单位)分别表示 $10$ 个苹果到地面的高度,两个相邻的整数之间用一个空格隔开。第二行只包括一个 $100$ 到 $120$ 之间(包含 $100$ 和 $120$ )的整数(以厘米为单位),表示陶陶把手伸直的时候能够达到的最大高度。
## 输出格式
输出包括一行,这一行只包含一个整数,表示陶陶能够摘到的苹果的数目。
## 样例 #1
### 样例输入 #1
```
100 200 150 140 129 134 167 198 200 111
110
```
### 样例输出 #1
```
5
```
## 提示
**【题目来源】**
NOIP 2005 普及组第一题满分答案:
package _01_入门阶段._02_数组基础.P1046陶陶摘苹果;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String[] inputs = sc.nextLine().split(" ");
int self_height= sc.nextInt();
int[] apple_heights = new int[inputs.length];
for (int i = 0; i < apple_heights.length; i++) {
apple_heights[i] = Integer.valueOf(inputs[i]);
}
int res =0;
for (int i = 0; i < apple_heights.length; i++) {
if(self_height+30>=apple_heights[i]){
res++;
}
}
System.out.println(res);
}
}校门外的树
# [NOIP2005 普及组] 校门外的树
## 题目描述
某校大门外长度为 $l$ 的马路上有一排树,每两棵相邻的树之间的间隔都是 $1$ 米。我们可以把马路看成一个数轴,马路的一端在数轴 $0$ 的位置,另一端在 $l$ 的位置;数轴上的每个整数点,即 $0,1,2,\dots,l$,都种有一棵树。
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。
## 输入格式
第一行有两个整数,分别表示马路的长度 $l$ 和区域的数目 $m$。
接下来 $m$ 行,每行两个整数 $u, v$,表示一个区域的起始点和终止点的坐标。
## 输出格式
输出一行一个整数,表示将这些树都移走后,马路上剩余的树木数量。
## 样例 #1
### 样例输入 #1
```
500 3
150 300
100 200
470 471
```
### 样例输出 #1
```
298
```
## 提示
**【数据范围】**
- 对于 $20\%$ 的数据,保证区域之间没有重合的部分。
- 对于 $100\%$ 的数据,保证 $1 \leq l \leq 10^4$,$1 \leq m \leq 100$,$0 \leq u \leq v \leq l$。
**【题目来源】**
NOIP 2005 普及组第二题满分答案:
package _01_入门阶段._02_数组基础.P1047校门外的树;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int l = sc.nextInt(), m = sc.nextInt();
// 长度为1的路可以种2棵树 ↑_↑
// 长度为4的路可以种5棵树 ↑_↑_↑_↑_↑
boolean[] road = new boolean[l + 1];
for (int i = 0; i < m; i++) {
int start = sc.nextInt();
int end = sc.nextInt();
for (int j = start; j <= end; j++) {
road[j] = true;
}
}
sc.close();
int res = 0;
for (int i = 0; i < road.length; i++) {
res += road[i] ? 0 : 1;
}
System.out.println(res);
}
}小鱼的数字游戏
# 小鱼的数字游戏
## 题目描述
小鱼最近被要求参加一个数字游戏,要求它把看到的一串数字 $a_i$(长度不一定,以 $0$ 结束),记住了然后反着念出来(表示结束的数字 $0$ 就不要念出来了)。这对小鱼的那点记忆力来说实在是太难了,你也不想想小鱼的整个脑袋才多大,其中一部分还是好吃的肉!所以请你帮小鱼编程解决这个问题。
## 输入格式
一行内输入一串整数,以 $0$ 结束,以空格间隔。
## 输出格式
一行内倒着输出这一串整数,以空格间隔。
## 样例 #1
### 样例输入 #1
```
3 65 23 5 34 1 30 0
```
### 样例输出 #1
```
30 1 34 5 23 65 3
```
## 提示
#### 数据规模与约定
对于 $100\%$ 的数据,保证 $0 \leq a_i \leq 2^{31} - 1$,数字个数不超过 $100$。满分答案:
package _01_入门阶段._02_数组基础.P1427小鱼的数字游戏;
import java.util.Scanner;
import java.util.Stack;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Stack<Integer> stack = new Stack<>();
while (true) {
int k = sc.nextInt();
if (k != 0) {
stack.push(k);
} else {
break;
}
}
while (!stack.isEmpty()) {
System.out.print(stack.pop());
if (stack.isEmpty()) {
System.out.print("\n");
}else{
System.out.print(" ");
}
}
}
}珠心算测验
# [NOIP2014 普及组] 珠心算测验
## 题目描述
珠心算是一种通过在脑中模拟算盘变化来完成快速运算的一种计算技术。珠心算训练,既能够开发智力,又能够为日常生活带来很多便利,因而在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加法能力的测验方法。他随机生成一个正整数集合,集合中的数各不相同,然后要求学生回答:其中有多少个数,恰好等于集合中另外两个(不同的)数之和?
最近老师出了一些测验题,请你帮忙求出答案。
(本题目为 2014NOIP 普及 T1)
## 输入格式
共两行,第一行包含一个整数 $n$,表示测试题中给出的正整数个数。
第二行有 $n$ 个正整数,每两个正整数之间用一个空格隔开,表示测试题中给出的正整数。
## 输出格式
一个整数,表示测验题答案。
## 样例 #1
### 样例输入 #1
```
4
1 2 3 4
```
### 样例输出 #1
```
2
```
## 提示
【样例说明】
由 $1+2=3,1+3=4$,故满足测试要求的答案为 $2$。
注意,加数和被加数必须是集合中的两个不同的数。
【数据说明】
对于 $100\%$ 的数据,$3 \leq n \leq 100$,测验题给出的正整数大小不超过 $10,000$。满分答案:
package _01_入门阶段._02_数组基础.P2141珠心算测验;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Scanner;
import java.util.Set;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
Map<Integer, Integer> numSet = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
nums[i] = sc.nextInt();
numSet.put(nums[i], i);
}
int res = 0;
for (int sum = 0; sum < nums.length; sum++) {
for (int i = 0; i < nums.length; i++) {
Integer j = numSet.get(nums[sum] - nums[i]);
if (j != null && i != j) {
res++;
break;// 找到一个即可
}
}
}
// 1+4=5 4+1=5 2+3=5 3+2=5 是一种不是四种
System.out.println(res);
}
public static void main_wrong(String[] args) {
// 错误写法:
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
Set<Integer> numSet = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
nums[i] = sc.nextInt();
numSet.add(nums[i]);
}
int res = 0;
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < nums.length; j++) {
if (i == j)
continue;
if (numSet.contains(nums[i] + nums[j])) {
res++;
}
}
}
System.out.println(res / 2/* a+b=b+a 被统计两次的不必再统计 */);
}
}【XR-4】模拟赛
# 【XR-4】模拟赛
## 题目描述
X 校正在进行 CSP 前的校内集训。
一共有 $n$ 名 OIer 参与这次集训,教练为他们精心准备了 $m$ 套模拟赛题。
然而,每名 OIer 都有各自的时间安排,巧合的是,他们在接下来的 $k$ 天中都恰好有 $m$ 天有空打模拟赛。
为了方便管理,教练规定一个人必须按顺序打完 $m$ 套模拟赛题。
比如,小 X 在接下来的第 $2,3,5$ 天有空打模拟赛,那么他就必须在第 $2$ 天打第 $1$ 套模拟赛题,第 $3$ 天打第 $2$ 套模拟赛题,第 $5$ 天打第 $3$ 套模拟赛题。
教练需要为每一个人的每一次模拟赛做准备,为了减小工作量,如果在某一天有多个人打同一套模拟赛题,那么教练只需要在这一天准备一场使用这一套题的模拟赛即可。
你作为机房大佬,教练想请你帮他计算一下,他每天需要准备多少场模拟赛。
## 输入格式
第一行三个整数 $n,m,k$。
接下来 $n$ 行,每行 $m$ 个整数,第 $i$ 行第 $j$ 列的整数 $a_{i,j}$ 表示第 $i$ 个人在接下来的 $k$ 天中第 $j$ 个有空的日子为第 $a_{i,j}$ 天。
## 输出格式
一行 $k$ 个整数,第 $i$ 个整数表示接下来的第 $i$ 天教练需要准备的模拟赛场数。
## 样例 #1
### 样例输入 #1
```
1 3 5
2 3 5
```
### 样例输出 #1
```
0 1 1 0 1
```
## 样例 #2
### 样例输入 #2
```
6 3 7
2 3 4
2 5 7
3 5 7
1 3 5
5 6 7
1 2 3
```
### 样例输出 #2
```
1 2 3 1 3 1 1
```
## 样例 #3
### 样例输入 #3
```
10 10 20
2 3 4 8 9 11 12 16 17 18
2 3 6 10 12 13 14 15 19 20
1 3 7 10 11 13 14 15 17 19
1 2 4 6 7 9 15 17 19 20
2 3 5 6 9 11 14 16 19 20
1 2 3 8 9 10 11 12 15 19
1 4 6 7 9 12 13 17 18 19
1 7 8 9 10 11 13 15 18 20
1 5 6 7 8 9 13 16 18 19
4 5 7 10 11 13 14 17 18 20
```
### 样例输出 #3
```
1 2 2 3 2 2 4 3 3 3 3 4 2 1 3 1 2 2 2 1
```
## 提示
**本题采用捆绑测试。**
- Subtask 1(13 points):$n = m = k = 1$。
- Subtask 2(24 points):$n = 1$。
- Subtask 3(24 points):$m = 1$。
- Subtask 4(39 points):无特殊限制。
对于 $100\%$ 的数据,$1 \le n,m,k \le 10^3$,$m \le k$,$1 \le a_{i,1} < a_{i,2} < \cdots < a_{i,m} \le k$。package _01_入门阶段._02_数组基础.P5594_XR_4模拟赛;
import java.util.Scanner;
public class Main {
// 这题主要就是要从题目弯弯绕绕的表述中理清题目要计算的本质东西是什么
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();// n个队员
int m = sc.nextInt();// m套题
int k = sc.nextInt();// 接下来有k天
int[] res = new int[k + 1];
boolean[][] sign = new boolean[k + 1][m + 1];// 用来标记sign[j][k] 第j天第k套题是否已经安排了考场
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 意思就是:第i个人的第j套题在第t天做
int t = sc.nextInt();
if (sign[t][j] == false) {
sign[t][j] = true;
res[t]++;
}
}
}
for (int i = 1; i <= k; i++) {
System.out.print(res[i]);
if(i!=k) System.out.print(" ");
else System.out.print("\n");
}
}
}Part 1.3 字符串基础
- P5015 标题统计
- P1055 ISBN号码
- P1308 统计单词数
- P2010 回文日期
- P1012 拼数
- P5587 打字练习
标题统计
# [NOIP2018 普及组] 标题统计
## 题目描述
凯凯刚写了一篇美妙的作文,请问这篇作文的标题中有多少个字符? 注意:标题中可能包含大、小写英文字母、数字字符、空格和换行符。统计标题字 符数时,空格和换行符不计算在内。
## 输入格式
输入文件只有一行,一个字符串 $s$。
## 输出格式
输出文件只有一行,包含一个整数,即作文标题的字符数(不含空格和换行符)。
## 样例 #1
### 样例输入 #1
```
234
```
### 样例输出 #1
```
3
```
## 样例 #2
### 样例输入 #2
```
Ca 45
```
### 样例输出 #2
```
4
```
## 提示
【输入输出样例 1 说明】
标题中共有 3 个字符,这 3 个字符都是数字字符。
【输入输出样例 2 说明】 标题中共有$ 5$ 个字符,包括 $1$ 个大写英文字母, $1$ 个小写英文字母和 $2$ 个数字字符, 还有 $1$ 个空格。由于空格不计入结果中,故标题的有效字符数为 $4$ 个。
【数据规模与约定】
规定 $|s|$ 表示字符串 $s$ 的长度(即字符串中的字符和空格数)。
对于 $40\%$ 的数据,$1 ≤ |s| ≤ 5$,保证输入为数字字符及行末换行符。
对于 $80\%$ 的数据,$1 ≤ |s| ≤ 5$,输入只可能包含大、小写英文字母、数字字符及行末换行符。
对于 $100\%$ 的数据,$1 ≤ |s| ≤ 5$,输入可能包含大、小写英文字母、数字字符、空格和行末换行符。package _01_入门阶段._03_字符串基础.P5015标题统计;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.nextLine();
int cnt = 0;
for(char ch:str.toCharArray()) {
if(!Character.isWhitespace(ch)) {
cnt++;
}
}
System.out.println(cnt);
}
}ISBN号码
# [NOIP2008 普及组] ISBN 号码
## 题目描述
每一本正式出版的图书都有一个 ISBN 号码与之对应,ISBN 码包括 $9$ 位数字、$1$ 位识别码和 $3$ 位分隔符,其规定格式如 `x-xxx-xxxxx-x`,其中符号 `-` 就是分隔符(键盘上的减号),最后一位是识别码,例如 `0-670-82162-4`就是一个标准的 ISBN 码。ISBN 码的首位数字表示书籍的出版语言,例如 $0$ 代表英语;第一个分隔符 `-` 之后的三位数字代表出版社,例如 $670$ 代表维京出版社;第二个分隔符后的五位数字代表该书在该出版社的编号;最后一位为识别码。
识别码的计算方法如下:
首位数字乘以 $1$ 加上次位数字乘以 $2$ ……以此类推,用所得的结果 $ \bmod 11$,所得的余数即为识别码,如果余数为 $10$,则识别码为大写字母 $X$。例如 ISBN 号码 `0-670-82162-4` 中的识别码 $4$ 是这样得到的:对 `067082162` 这 $9$ 个数字,从左至右,分别乘以 $1,2,\dots,9$ 再求和,即 $0\times 1+6\times 2+……+2\times 9=158$,然后取 $158 \bmod 11$ 的结果 $4$ 作为识别码。
你的任务是编写程序判断输入的 ISBN 号码中识别码是否正确,如果正确,则仅输出 `Right`;如果错误,则输出你认为是正确的 ISBN 号码。
## 输入格式
一个字符序列,表示一本书的 ISBN 号码(保证输入符合 ISBN 号码的格式要求)。
## 输出格式
一行,假如输入的 ISBN 号码的识别码正确,那么输出 `Right`,否则,按照规定的格式,输出正确的 ISBN 号码(包括分隔符 `-`)。
## 样例 #1
### 样例输入 #1
```
0-670-82162-4
```
### 样例输出 #1
```
Right
```
## 样例 #2
### 样例输入 #2
```
0-670-82162-0
```
### 样例输出 #2
```
0-670-82162-4
```
## 提示
2008 普及组第一题package _01_入门阶段._03_字符串基础.P1055_ISBN号码;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String ISBN = sc.nextLine();//x-xxx-xxxxx-x
int k = 1;
int s = 0;
for (int i = 0; i < ISBN.length()-1; i++) {
char ch = ISBN.charAt(i);
if(ch=='-')continue;
int n = ch-'0';
s+=(n*k++)%11;
}
s%=11;
char correntEnd = (char)(s==10? 'X':s+'0');
if(correntEnd==ISBN.charAt(ISBN.length()-1)) {
System.out.println("Right");
}else {
StringBuilder sBuilder = new StringBuilder();
sBuilder.append(ISBN);
sBuilder.setCharAt(sBuilder.length()-1, correntEnd);
System.out.println(sBuilder.toString());
}
}
}统计单词数
# [NOIP2011 普及组] 统计单词数
## 题目描述
一般的文本编辑器都有查找单词的功能,该功能可以快速定位特定单词在文章中的位置,有的还能统计出特定单词在文章中出现的次数。
现在,请你编程实现这一功能,具体要求是:给定一个单词,请你输出它在给定的文章中出现的次数和第一次出现的位置。注意:匹配单词时,不区分大小写,但要求完全匹配,即给定单词必须与文章中的某一独立单词在不区分大小写的情况下完全相同(参见样例 1),如果给定单词仅是文章中某一单词的一部分则不算匹配(参见样例 2)。
## 输入格式
共 $2$ 行。
第 $1$ 行为一个字符串,其中只含字母,表示给定单词;
第 $2$ 行为一个字符串,其中只可能包含字母和空格,表示给定的文章。
## 输出格式
一行,如果在文章中找到给定单词则输出两个整数,两个整数之间用一个空格隔开,分别是单词在文章中出现的次数和第一次出现的位置(即在文章中第一次出现时,单词首字母在文章中的位置,位置从 $0$ 开始);如果单词在文章中没有出现,则直接输出一个整数 $-1$。
## 样例 #1
### 样例输入 #1
```
To
to be or not to be is a question
```
### 样例输出 #1
```
2 0
```
## 样例 #2
### 样例输入 #2
```
to
Did the Ottoman Empire lose its power at that time
```
### 样例输出 #2
```
-1
```
## 提示
数据范围
$1\leq $ 第一行单词长度 $\leq10$。
$1\leq $ 文章长度 $\leq10^6$。
noip2011 普及组第 2 题package _01_入门阶段._03_字符串基础.P1308统计单词数;
import java.util.Scanner;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String target = sc.nextLine().toLowerCase();
String content = sc.nextLine().toLowerCase();
String regex = "\\b"+target+"\\b";
Pattern p = Pattern.compile(regex);
Matcher m = p.matcher(content); // 获取 matcher 对象
int idx = -1;
int cnt = 0;
while(m.find()) {
if(idx==-1) {
idx=m.start();
}
cnt++;
}
if(idx!=-1) {
System.out.println(cnt+" "+idx);
}else {
System.out.println(-1);
}
}
}回文日期
# [NOIP2016 普及组] 回文日期
## 题目背景
NOIP2016 普及组 T2
## 题目描述
在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用 $8$ 位数字表示一个日期,其中,前 $4$ 位代表年份,接下来 $2$ 位代表月份,最后 $2$ 位代表日期。显然:一个日期只有一种表示方法,而两个不同的日期的表 示方法不会相同。
牛牛认为,一个日期是回文的,当且仅当表示这个日期的 $8$ 位数字是回文的。现在,牛牛想知道:在他指定的两个日期之间包含这两个日期本身),有多少个真实存在的日期是回文的。
一个 $8$ 位数字是回文的,当且仅当对于所有的 $i$($1 \le i \le 8$)从左向右数的第 $i$ 个数字和第 $9-i$ 个数字(即从右向左数的第 $i$ 个数字)是相同的。
例如:
- 对于 2016 年 11 月 19 日,用 $8$ 位数字 $20161119$ 表示,它不是回文的。
- 对于 2010 年 1 月 2 日,用 $8$ 位数字 $20100102$ 表示,它是回文的。
- 对于 2010 年 10 月 2 日,用 $8$ 位数字 $20101002$ 表示,它不是回文的。
每一年中都有 $12$ 个月份:
其中,$1, 3, 5, 7, 8, 10, 12$ 月每个月有 $31$ 天;$4, 6, 9, 11$ 月每个月有 $30$ 天;而对于 $2$ 月,闰年时有 $29$ 天,平年时有 $28$ 天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种:
1. 这个年份是 $4$ 的整数倍,但不是 $100$ 的整数倍;
2. 这个年份是 $400$ 的整数倍。
例如:
- 以下几个年份都是闰年:$2000, 2012, 2016$。
- 以下几个年份是平年:$1900, 2011, 2014$。
## 输入格式
两行,每行包括一个 $8$ 位数字。
第一行表示牛牛指定的起始日期。
第二行表示牛牛指定的终止日期。
保证 $\mathit{date}_1$ 和 $\mathit{date}_2$ 都是真实存在的日期,且年份部分一定为 $4$ 位数字,且首位数字不为 $0$。
保证 $\mathit{date}_1$ 一定不晚于 $\mathit{date}_2$。
## 输出格式
一个整数,表示在 $\mathit{date}_1$ 和 $\mathit{date}_2$ 之间,有多少个日期是回文的。
## 样例 #1
### 样例输入 #1
```
20110101
20111231
```
### 样例输出 #1
```
1
```
## 样例 #2
### 样例输入 #2
```
20000101
20101231
```
### 样例输出 #2
```
2
```
## 提示
**【样例说明】**
对于样例 1,符合条件的日期是 $20111102$。
对于样例 2,符合条件的日期是 $20011002$ 和 $20100102$。
**【子任务】**
对于 $60 \%$ 的数据,满足 $\mathit{date}_1 = \mathit{date}_2$。package _01_入门阶段._03_字符串基础.P2010_回文日期;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int from = sc.nextInt();
int to = sc.nextInt();
int cnt = 0;
for (int cur = from; cur <= to; cur = getNextDate(cur)) {
String s1 = cur + "";
String s2 = new StringBuffer(s1).reverse().toString();
if (s1.equals(s2)) {
cnt++;
}
}
System.out.println(cnt);
}
// 获取下一个日期
static int getNextDate(int date) {
// date:年年年月月日日
// 润年:被400整除||(被4整除&&不被100整除)
// 2月润28天平29天
// 4 6 9 11月30天,
// 其他月31天
int yyyy = date / 10000;
int mm = date / 100 % 100;
int dd = date % 100;
dd++;
switch (mm) {
case 2:
if (isRunYear(yyyy)) {
if (dd == 30/* 闰年2月正常应该29天,30天说明应该进位了 */) {
dd = 1;
mm++;
}
} else {
if (dd == 29/* 正常应该28天,29天说明应该进位了 */) {
dd = 1;
mm++;
}
}
break;
case 4:
case 6:
case 9:
case 11:
if (dd == 31/* 正常应该30天,31天说明应该进位了 */) {
dd = 1;
mm++;
}
break;
default:
if (dd == 32/* 正常应该31天,32天说明应该进位了 */) {
dd = 1;
mm++;
}
break;
}
if (mm == 13/* 正常最多12月,13说明应该进位了 */) {
mm = 1;
yyyy++;
}
return yyyy * 10000 + mm * 100 + dd;
}
static boolean isRunYear(int yyyy) {
return yyyy % 400 == 0 || (yyyy % 4 == 0 && yyyy % 100 != 0);
}
}拼数
# [NOIP1998 提高组] 拼数
## 题目描述
设有 $n$ 个正整数 $a_1 \dots a_n$,将它们联接成一排,相邻数字首尾相接,组成一个最大的整数。
## 输入格式
第一行有一个整数,表示数字个数 $n$。
第二行有 $n$ 个整数,表示给出的 $n$ 个整数 $a_i$。
## 输出格式
一个正整数,表示最大的整数
## 样例 #1
### 样例输入 #1
```
3
13 312 343
```
### 样例输出 #1
```
34331213
```
## 样例 #2
### 样例输入 #2
```
4
7 13 4 246
```
### 样例输出 #2
```
7424613
```
## 提示
对于全部的测试点,保证 $1 \leq n \leq 20$,$1 \leq a_i \leq 10^9$。package _01_入门阶段._03_字符串基础.P1012_拼数;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
Integer[] nums = new Integer[N];
for (Integer i = 0; i < nums.length; i++) {
nums[i] = sc.nextInt();
}
Arrays.sort(nums, (o1, o2) -> {
// 这句排序算法是关键
return -("" + o1 + o2).compareTo("" + o2 + o1);
// 错误写法:
// o1 太大了,加起来更大
// return -Integer.compare(Integer.valueOf(o1 + "" + o2), Integer.valueOf(o2 + "" + o1));
});
StringBuilder sb = new StringBuilder();
for (int i = 0; i < nums.length; i++) {
sb.append(nums[i] + "");
}
System.out.println(sb.toString());
}
}打字练习
# 打字练习
## 题目描述
R 君在练习打字。
有这样一个打字练习网站,给定一个范文和输入框,会根据你的输入计算准确率和打字速度。可以输入的字符有小写字母、空格和 `.`(英文句号),输入字符后,光标也会跟着移动。
输入的文本有多行,R 君可以通过换行键来换行,换行后光标移动到下一行的开头。
R 君也可以按退格键(为了方便,退格键用 `<` 表示),以删除上一个打的字符,并将光标回移一格。特殊的,如果此时光标已经在一行的开头,则不能继续退格(即忽略此时输入的退格键)。
网站的比较方式遵循以下两个原则:
- 逐行比较,即对于范文和输入的每一行依次比较,不同行之间不会产生影响,多余的行会被忽略。
- 逐位比较,即对于两行的每一个字符依次比较,当且仅当字符相同时才会被算作一次正确,否则会被算作错误。计算答案时,只统计相同的字符个数。
需要注意的是,回车键不会被计入正确的字符个数。
R 君看到网站上显示他花了 $T$ 秒完成了这次的打字游戏,请你计算出他的 KPM(Keys per minutes,每分钟输入的字符个数),答案四舍五入保留整数部分。
## 输入格式
R 君会依次告诉你网站的范文,他的输入和花费的时间。
其中范文和输入将会这样读入:给定若干行字符串,以单独的一行 `EOF` 结束,其中 `EOF` 不算入输入的文本。
最后一行一个整数 $T$,表示他打字花费了 $T$ 秒。
可以参考样例输入输出文件和样例解释辅助理解。
## 输出格式
一行一个整数,表示 KPM。
## 样例 #1
### 样例输入 #1
```
hello world.
aaabbbb
x
EOF
heelo world.
aaacbbbb
y<x
EOF
60
```
### 样例输出 #1
```
18
```
## 提示
#### 样例解释
第一行的正确字符数为 11。
第二行的正确字符数为 6,错误的字符 `c` 仍会占据一个位置。
第三行的正确字符数为 1,R 君使用退格键删除了被打错的字符 `y`
#### 数据范围
对于 $20\%$ 的数据,不存在换行键。
对于 $40\%$ 的数据,不存在退格键。
对于 $100\%$ 的数据,$T \leq 10^3$,保证每个文本段的总字符数(包括换行)不超过 $10^5$ 个且总行数不超过 $10^4$。package _01_入门阶段._03_字符串基础.P5587_打字练习;
import java.util.LinkedList;
import java.util.Scanner;
import java.util.Stack;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
LinkedList<String> article = new LinkedList<>();
LinkedList<String> inputs = new LinkedList<>();
String line;
// 这题最坑的就是范文也有‘<’退格键需要处理。
while (!(line = sc.nextLine()).equals("EOF")) {
Stack<Character> buffer = new Stack<>();// 缓冲区
for (char ch : line.toCharArray()) {
if (ch == '<') {// 删除键
if (buffer.size() > 0)
buffer.pop();// 清除缓冲区中的一个元素
} else {
buffer.push(ch);// 录入非删除键
}
}
StringBuffer sb = new StringBuffer();
for (char ch : buffer) {
sb.append(ch);
}
article.add(sb.toString());
}
while (!(line = sc.nextLine()).equals("EOF")) {
Stack<Character> buffer = new Stack<>();// 缓冲区
for (char ch : line.toCharArray()) {
if (ch == '<') {// 删除键
if (buffer.size() > 0)
buffer.pop();// 清除缓冲区中的一个元素
} else {
buffer.push(ch);// 录入非删除键
}
}
StringBuffer sb = new StringBuffer();
for (char ch : buffer) {
sb.append(ch);
}
inputs.add(sb.toString());
}
int Ts = sc.nextInt();
int cnt = 0;
// System.out.println(article);
// System.out.println(inputs);
while (article.size() != 0 && inputs.size() != 0) {
String lineA = article.removeFirst();
String lineB = inputs.removeFirst();
int i = 0;
while (i < lineA.length() && i < lineB.length()) {
if (lineA.charAt(i) == lineB.charAt(i)) {
cnt++;
}
i++;
}
}
int res = (int) (cnt / (Ts / 60.0) + 0.5);// 四舍五入直接+0.5然后强制转int即可
System.out.println(res);
}
}Part 1.4 函数,递归及递推
- P1028 数的计算
- P1036 选数
- P1464 Function
- P5534 【XR-3】等差数列
- P1192 台阶问题
- P1025 数的划分
- P4994 终于结束的起点
数的计算
# [NOIP2001 普及组] 数的计算
## 题目描述
给出自然数 $n$,要求按如下方式构造数列:
1. 只有一个数字 $n$ 的数列是一个合法的数列。
2. 在一个合法的数列的末尾加入一个自然数,但是这个自然数不能超过该数列最后一项的一半,可以得到一个新的合法数列。
请你求出,一共有多少个合法的数列。两个合法数列 $a, b$ 不同当且仅当两数列长度不同或存在一个正整数 $i \leq |a|$,使得 $a_i \neq b_i$。
## 输入格式
输入只有一行一个整数,表示 $n$。
## 输出格式
输出一行一个整数,表示合法的数列个数。
## 样例 #1
### 样例输入 #1
```
6
```
### 样例输出 #1
```
6
```
## 提示
### 样例 1 解释
满足条件的数列为:
- $6$
- $6, 1$
- $6, 2$
- $6, 3$
- $6, 2, 1$
- $6, 3, 1$
### 数据规模与约定
对于全部的测试点,保证 $1 \leq n \leq 10^3$。
### 说明
本题数据来源是 NOIP 2001 普及组第一题,但是原题的题面描述和数据不符,故对题面进行了修改,使之符合数据。原题面如下,谨供参考:
> 我们要求找出具有下列性质数的个数(包含输入的正整数 $n$)。
>
> 先输入一个正整数 $n$($n \le 1000$),然后对此正整数按照如下方法进行处理:
>
> 1. 不作任何处理;
> 2. 在它的左边拼接一个正整数,但该正整数不能超过原数,或者是上一个被拼接的数的一半;
> 3. 加上数后,继续按此规则进行处理,直到不能再加正整数为止。
感谢 @[dbxxx](/user/120868) 对本题情况的反馈,原题面的问题见[本贴](https://www.luogu.com.cn/discuss/526184)。package _01_入门阶段._04_函数_递归及递推._01_P1028数的计算;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(dfs(sc.nextInt()));
}
static Map<Integer, Integer> cacheMap = new HashMap<>();
static int dfs(int cur_last) {
if(cacheMap.containsKey(cur_last)) {
return cacheMap.get(cur_last);
}
int res=0;
// 情况1:不往后添加新数
res+=1;
// 情况2:往后添加新数
for (int next = cur_last/2; 1 <= next ; next--) {
res+=dfs(next);
}
cacheMap.put(cur_last, res);// 缓存
return res;
}
}选数
# [NOIP2002 普及组] 选数
## 题目描述
已知 $n$ 个整数 $x_1,x_2,\cdots,x_n$,以及 $1$ 个整数 $k$($k<n$)。从 $n$ 个整数中任选 $k$ 个整数相加,可分别得到一系列的和。例如当 $n=4$,$k=3$,$4$ 个整数分别为 $3,7,12,19$ 时,可得全部的组合与它们的和为:
$3+7+12=22$
$3+7+19=29$
$7+12+19=38$
$3+12+19=34$
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:$3+7+19=29$。
## 输入格式
第一行两个空格隔开的整数 $n,k$($1 \le n \le 20$,$k<n$)。
第二行 $n$ 个整数,分别为 $x_1,x_2,\cdots,x_n$($1 \le x_i \le 5\times 10^6$)。
## 输出格式
输出一个整数,表示种类数。
## 样例 #1
### 样例输入 #1
```
4 3
3 7 12 19
```
### 样例输出 #1
```
1
```
## 提示
**【题目来源】**
NOIP 2002 普及组第二题package _01_入门阶段._04_函数_递归及递推._02_P1036_选数;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
nums = new int[N];
for (int i = 0; i < nums.length; i++) {
nums[i] = sc.nextInt();
}
dfs(0, 0, 0);
System.out.println(cnt);
}
static int N;
static int K;
static int cnt = 0;
static int[] nums;
static void dfs(int curIdx/* 递归考虑每一个数选或不选两种情况 */, int sum, int selected) {
if (selected == K) {
if (isPrime(sum)) {
cnt++;
}
} else {
if (curIdx < nums.length) {
// 考虑当前位置的数:
// 不选该数
dfs(curIdx + 1, sum, selected);
// 选择该数
dfs(curIdx + 1, sum + nums[curIdx], selected + 1);
}
}
}
private static boolean isPrime(int num) {
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
}Function
# Function
## 题目描述
对于一个递归函数 $w(a,b,c)$
- 如果 $a \le 0$ 或 $b \le 0$ 或 $c \le 0$ 就返回值$ 1$。
- 如果 $a>20$ 或 $b>20$ 或 $c>20$ 就返回 $w(20,20,20)$
- 如果 $a<b$ 并且 $b<c$ 就返回$ w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c)$。
- 其它的情况就返回 $w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1)$
这是个简单的递归函数,但实现起来可能会有些问题。当 $a,b,c$ 均为 $15$ 时,调用的次数将非常的多。你要想个办法才行。
注意:例如 $w(30,-1,0)$ 又满足条件 $1$ 又满足条件 $2$,请按照最上面的条件来算,答案为 $1$。
## 输入格式
会有若干行。
并以 $-1,-1,-1$ 结束。
## 输出格式
输出若干行,每一行格式:
`w(a, b, c) = ans`
注意空格。
## 样例 #1
### 样例输入 #1
```
1 1 1
2 2 2
-1 -1 -1
```
### 样例输出 #1
```
w(1, 1, 1) = 2
w(2, 2, 2) = 4
```
## 提示
### 数据规模与约定
保证输入的数在 $[-9223372036854775808,9223372036854775807]$ 之间,并且是整数。
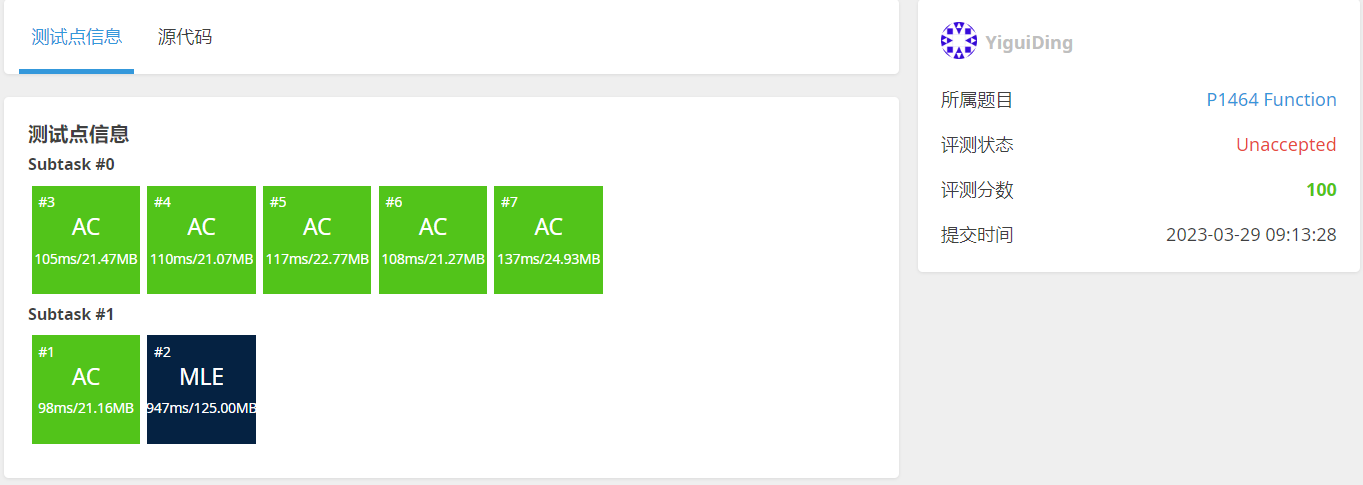
保证不包括 $-1, -1, -1$ 的输入行数 $T$ 满足 $1 \leq T \leq 10 ^ 5$。写法1:内存超过限制
package _01_入门阶段._04_函数_递归及递推._03_P1464_Function;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long a, b, c;
while (true) {
a = sc.nextLong();
b = sc.nextLong();
c = sc.nextLong();
if (a == -1 && b == -1 && c == -1) {
break;
}
System.out.println("w(" + a + ", " + b + ", " + c + ") = " + w(a, b, c));
// System.out.printf("w(%d, %d, %d) = %d\n", a, b, c, w(a, b, c));
}
sc.close();
}
static Map<State, Long> cache = new HashMap<>();
static long w(long a, long b, long c) {
if (a <= 0 || b <= 0 || c <= 0) {
return 1;
} else if (a > 20 || b > 20 | c > 20) {
return w(20, 20, 20);
}
State state = new State(a, b, c);
if (cache.containsKey(state)) {
return cache.get(state);
}
long res = 0;
if (a < b && b < c) {
res = w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
} else {
res = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1);
}
cache.put(state, res);
return res;
}
static class State {
long a, b, c;
public State(long a, long b, long c) {
this.a = a;
this.b = b;
this.c = c;
}
@Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = prime * result + (int) (a ^ (a >>> 32));
result = prime * result + (int) (b ^ (b >>> 32));
result = prime * result + (int) (c ^ (c >>> 32));
return result;
}
@Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
State other = (State) obj;
if (a != other.a)
return false;
if (b != other.b)
return false;
if (c != other.c)
return false;
return true;
}
}
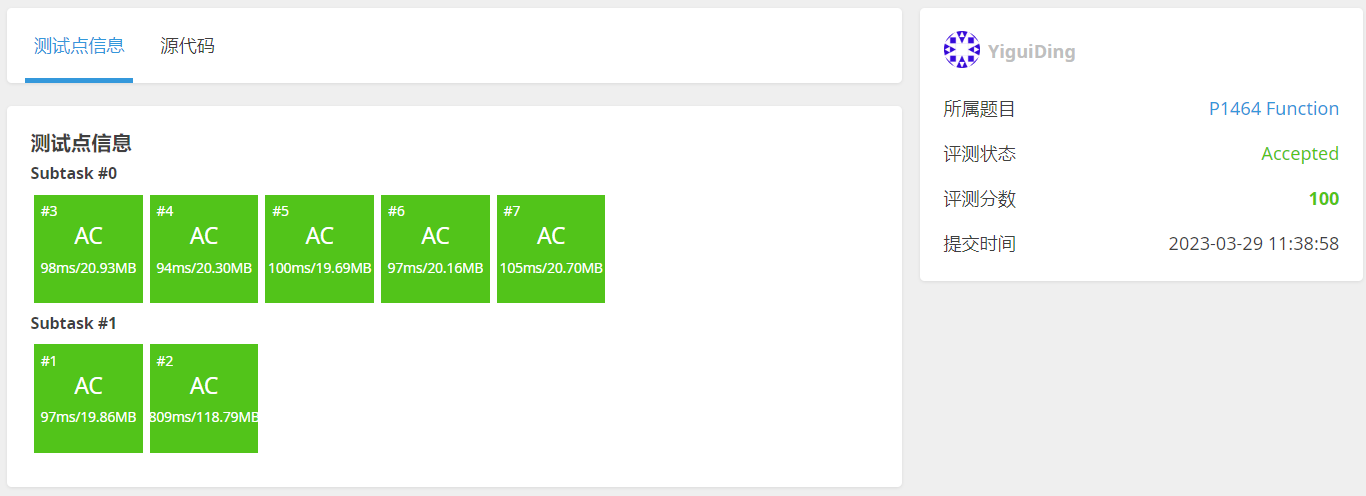
}写法2:可以通过,但如果使用printf则会超时
package _01_入门阶段._04_函数_递归及递推._03_P1464_Function;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long a, b, c;
while (true) {
a = sc.nextLong();
b = sc.nextLong();
c = sc.nextLong();
if (a == -1 && b == -1 && c == -1) {
break;
}
// 100分通过测试的写法 最后一个测试点可以通过 消耗:799ms/118.28MB
System.out.println("w(" + a+ ", "+ b+", "+c +") = "+ w(a, b, c));
// 不知道为什么,这样写最后一个测试点无法通过,提示超时 消耗:1.20s/120.30MB
// System.out.printf("w(%d, %d, %d) = %d%n", a, b, c, w(a, b, c));
}
sc.close();
}
static long[][][] cache = new long[21][21][21];
static boolean[][][] computed = new boolean[21][21][21];
static long w(long a, long b, long c) {
if (a <= 0 || b <= 0 || c <= 0) {
return 1;
}
if (a > 20 || b > 20 | c > 20) {
return w(20, 20, 20);
}
if (computed[(int) a][(int) b][(int) c]) {
return cache[(int) a][(int) b][(int) c];
}
long res;
if (a < b && b < c) {
res = w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
} else {
res = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1);
}
cache[(int) a][(int) b][(int) c] = res;
computed[(int) a][(int) b][(int) c] = true;
return res;
}
}等差数列
# 【XR-3】等差数列
## 题目描述
小 X 给了你一个等差数列的前两项以及项数,请你求出这个等差数列各项之和。
等差数列:对于一个 $n$ 项数列 $a$,如果满足对于任意 $i \in [1,n)$,有 $a_{i+1} - a_i = d$,其中 $d$ 为定值,则称这个数列为一个等差数列。
## 输入格式
一行 $3$ 个整数 $a_1, a_2, n$,表示等差数列的第 $1,2$ 项以及项数。
**数据范围:**
- $|a_1|,|a_2| \le 10^6$。
- $3 \le n \le 10^6$。
## 输出格式
一行一个整数,表示答案。
## 样例 #1
### 样例输入 #1
```
1 2 3
```
### 样例输出 #1
```
6
```
## 样例 #2
### 样例输入 #2
```
-5 -10 5
```
### 样例输出 #2
```
-75
```
## 提示
【样例 $1$ 说明】
这个等差数列为 `1 2 3`,其各项之和为 $6$。package _01_入门阶段._04_函数_递归及递推._03_P5534_XR_3_等差数列;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long a1 = sc.nextLong();
long a2 = sc.nextLong();
long n = sc.nextLong();
sc.close();
long d = a2 - a1;// 计算公差
long a_n = a1 + (n - 1) * d;// 计算第n项
long sum_n = (a1 + a_n) * n / 2;// 等差数列求和公式
System.out.println(sum_n);
}
}台阶问题
# 台阶问题
## 题目描述
有 $N$ 级台阶,你一开始在底部,每次可以向上迈 $1\sim K$ 级台阶,问到达第 $N$ 级台阶有多少种不同方式。
## 输入格式
两个正整数 $N,K$。
## 输出格式
一个正整数 $ans\pmod{100003}$,为到达第 $N$ 级台阶的不同方式数。
## 样例 #1
### 样例输入 #1
```
5 2
```
### 样例输出 #1
```
8
```
## 提示
- 对于 $20\%$ 的数据,$1\leq N\leq10$,$1\leq K\leq3$;
- 对于 $40\%$ 的数据,$1\leq N\leq1000$;
- 对于 $100\%$ 的数据,$1\leq N\leq100000$,$1\leq K\leq100$。动态规划写法
package _01_入门阶段._04_函数_递归及递推._04_P1192_台阶问题_动态规划写法;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int K = sc.nextInt();
sc.close();
int[][] dp = new int[N + 1][K + 1];
// dp[len][step] = 路长为len 走step步有dp[len][step]种方法
// dp[len][step] 当 len==step时,dp[len][step]=1;
// dp[len][step] = sum(dp[len-step])
for (int len = 1; len <= N; len++) {
for (int step = 1; step <= K; step++) {
if (len == step) {
dp[len][step] = 1;
} else if (len > step) {
dp[len][step] = arrSum(dp[len - step]) % MOD;
}
}
}
int res = arrSum(dp[N]) % MOD;
System.out.print(res);
}
static int arrSum(int[] arr) {
int sum = 0;
for (int i = 0; i < arr.length; i++) {
sum += arr[i];
}
return sum;
}
static int MOD = 100003;
}递归写法
package _01_入门阶段._04_函数_递归及递推._04_P1192_台阶问题_递归写法;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
sc.close();
computed = new boolean[N];
cache = new int[N];
System.out.println(dfs(0));
}
static int N;
static int K;
static boolean[] computed;// 标记该位置有没有计算出来
static int[] cache;// 缓存
static int MOD = 100003;
static int dfs(int curPos) {
if (curPos == N) {
return 1;
} else if (curPos < N) {
if (computed[curPos])
return cache[curPos];
int cnt = 0;
for (int step = 1; step <= K; step++) {
cnt += dfs(curPos + step) % MOD;
cnt %= MOD;
}
cache[curPos] = cnt;// 缓存
computed[curPos] = true;// 标记为已经计算过了
return cnt;
} else
return 0;
}
}数的划分
# [NOIP2001 提高组] 数的划分
## 题目描述
将整数 $n$ 分成 $k$ 份,且每份不能为空,任意两个方案不相同(不考虑顺序)。
例如:$n=7$,$k=3$,下面三种分法被认为是相同的。
$1,1,5$;
$1,5,1$;
$5,1,1$.
问有多少种不同的分法。
## 输入格式
$n,k$ ($6<n \le 200$,$2 \le k \le 6$)
## 输出格式
$1$ 个整数,即不同的分法。
## 样例 #1
### 样例输入 #1
```
7 3
```
### 样例输出 #1
```
4
```
## 提示
四种分法为:
$1,1,5$;
$1,2,4$;
$1,3,3$;
$2,2,3$.
**【题目来源】**
NOIP 2001 提高组第二题package _01_入门阶段._04_函数_递归及递推._05_P1025_数的划分;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
cache = new int[N + 1][N + 1][K + 1];
computed = new boolean[N + 1][N + 1][K + 1];
System.out.println(dfs(1, 0, 0));
}
static int N;
static int K;
static LinkedList<Integer> result = new LinkedList<>();
static int[][][] cache;
static boolean[][][] computed;
static int dfs(int curNum, int curSum, int selected) {
if (curSum > N/* 剪枝,和大于目标值提前结束递归 */ || curNum > N/* 数字的范围1+7=8 7是组成8的最大的数 */) {
return 0;
}
if (selected == K) {
if (curSum == N) {
// System.out.println(result);
return 1;
} else {
return 0;
}
} else {
if (computed[curNum][curSum][selected]) {// 查缓存
return cache[curNum][curSum][selected];
}
int cnt = 0;
// 不选当前数
cnt += dfs(curNum + 1/* 后续也不再考虑这个数 */, curSum, selected);
// 选当前数
// result.add(curNum);
cnt += dfs(
curNum/* 后续任然可能选择当前数,但绝不会再选择之前的数导致重复 */,
curSum + curNum/* 求和 */,
selected + 1/* 选中 */
);
// result.removeLast();
cache[curNum][curSum][selected] = cnt;// 缓存
computed[curNum][curSum][selected] = true;
return cnt;
}
}
}终于结束的起点
# 终于结束的起点
## 题目背景
> 终于结束的起点
> 终于写下句点
> 终于我们告别
> 终于我们又回到原点
> ……
一个个 OIer 的竞赛生涯总是从一场 NOIp 开始,大多也在一场 NOIp 中结束,好似一次次轮回在不断上演。
如果这次 NOIp 是你的起点,那么祝你的 OI 生涯如同夏花般绚烂。
如果这次 NOIp 是你的终点,那么祝你的 OI 回忆宛若繁星般璀璨。
也许这是你最后一次在洛谷上打比赛,也许不是。
不过,无论如何,祝你在一周后的比赛里,好运。
当然,这道题也和轮回有关系。
## 题目描述
广为人知的斐波拉契数列 $\mathrm{fib}(n)$ 是这么计算的
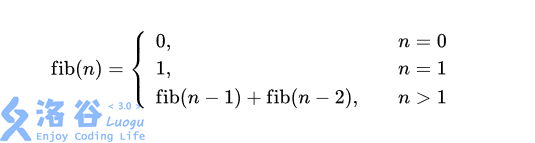
也就是 $0, 1, 1, 2, 3, 5, 8, 13 \cdots$,每一项都是前两项之和。
小 F 发现,如果把斐波拉契数列的每一项对任意大于 $1$ 的正整数 $M$ 取模的时候,数列都会产生循环。
当然,小 F 很快就明白了,因为 ($\mathrm{fib}(n - 1) \bmod M$) 和 ($\mathrm{fib}(n - 2) \bmod M)$ 最多只有 $M ^ 2$ 种取值,所以在 $M ^ 2$ 次计算后一定出现过循环。
甚至更一般地,我们可以证明,无论取什么模数 $M$,最终模 $M$ 下的斐波拉契数列都会是 $0, 1, \cdots, 0, 1, \cdots$。
现在,给你一个模数 $M$,请你求出最小的 $n > 0$,使得 $\mathrm{fib}(n) \bmod M = 0, \mathrm{fib}(n + 1) \bmod M = 1$。
## 输入格式
输入一行一个正整数 $M$。
## 输出格式
输出一行一个正整数 $n$。
## 样例 #1
### 样例输入 #1
```
2
```
### 样例输出 #1
```
3
```
## 样例 #2
### 样例输入 #2
```
6
```
### 样例输出 #2
```
24
```
## 提示
#### 样例 1 解释
斐波拉契数列为 $0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \cdots$,在对 $2$ 取模后结果为 $0, 1, 1, 0, 1, 1, 0, 1, 1, 0, \cdots$。
我们可以发现,当 $n = 3$ 时,$f(n) \bmod 2= 0, f(n + 1) \bmod 2 = 1$,也就是我们要求的 $n$ 的最小值。
#### 数据范围
对于 $30\%$ 的数据,$M \leq 18$;
对于 $70\%$ 的数据,$M \leq 2018$;
对于 $100\%$ 的数据,$2 \leq M \leq 706150=$`0xAC666`。
#### 提示
如果你还不知道什么是取模 $(\bmod)$,那我也很乐意告诉你,模运算是求整数除法得到的余数,也就是竖式除法最终「除不尽」的部分,也即
$$a \bmod M =k \iff a = bM + k\ (M > 0, 0 \leq k < M)$$
其中 $a, b, k$ 都是非负整数。
如果你使用 `C` / `C++`,你可以使用 `%` 来进行模运算。
如果你使用 `Pascal`,你可以使用 `mod` 来进行模运算。package _01_入门阶段._04_函数_递归及递推._06_P4994_终于结束的起点;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Mod = sc.nextInt();
FibGen gen = new FibGen();
gen.gen();
int preN = gen.idx;
int preF = gen.fib;
while (true) {
gen.gen();
int curN = gen.idx;
int curF = gen.fib;
if (preF % Mod == 0 && curF % Mod == 1) {
break;
}
preF = curF;
preN = curN;
}
System.out.println(preN);
}
static int Mod;
static class FibGen {
// fib: +5 -3 +2 -1 +1 0 1 1 2
// idx: -5 -4 -3 -2 -1 0 1 2 3
int a = -1;
int b = 1;
int fib = a + b;
int idx = 0;
public void gen() {
a = b;
b = fib;
fib = a + b;
fib %= Mod;// 直接取余
idx++;
}
}
}Part 2 基础算法
这一部分的内容包含了 OI 中的基础算法,供各位巩固基础。
当然,这里面也有一些难度比较高的题目。
Part 2.1 模拟
模拟,顾名思义就是题目要求你做什么你就做什么,这样的题目很考验选手的代码组织能力。
这里不仅仅有非常基础的模拟,也有一些非常复杂的题目。
- P1003 铺地毯
- P1067 多项式输出
- P1328 生活大爆炸版石头剪刀布
- P1563 玩具谜题
- P1042 乒乓球
- P1179 数字统计
- P2615 神奇的幻方
- P3952 时间复杂度
- P2482 [SDOI2010]猪国杀
- P5380 [THUPC2019]鸭棋
铺地毯
100分写法2
package _02_基础算法._01_模拟._01_P1003铺地毯_3_满分;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
Stack<React> stack = new Stack<>();
for (int i = 1; i <= N; i++) {
stack.add(new React(sc.nextInt(), sc.nextInt(), sc.nextInt(), sc.nextInt()));
}
Point point = new Point(sc.nextInt(), sc.nextInt());
int n = N;
while (!stack.isEmpty()) {
React react = stack.pop();
if (point.isCollision(react)) {
System.out.println(n);
return;
}
n--;
}
System.out.println(-1);
}
}
class React {
int x, y, w, h;
React(int xx, int yy, int ww, int hh) {
this.x = xx;
this.y = yy;
this.w = ww;
this.h = hh;
}
}
class Point {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
boolean isCollision(React react) {
return react.x <= x && x <= react.x + react.w &&
react.y <= y && y <= react.y + react.h;
}
}100分写法1
package _02_基础算法._01_模拟._01_P1003铺地毯_2_满分;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = Integer.parseInt(sc.nextLine());
Stack<String> stack = new Stack<>();
for (int i = 1; i <= N; i++) {
stack.push(sc.nextLine());
}
String[] pos = sc.nextLine().split(" ");
Point point = new Point(Integer.parseInt(pos[0]), Integer.parseInt(pos[1]));
int n = N;
while (!stack.isEmpty()) {
String[] nums = stack.pop().split(" ");
React react = new React(
Integer.parseInt(nums[0]),
Integer.parseInt(nums[1]),
Integer.parseInt(nums[2]),
Integer.parseInt(nums[3]));
if (point.isCollision(react)) {
break;
}
n--;
}
if (n != 0) {
System.out.println(n);
} else
System.out.println(-1);
}
}
class React {
int x, y, w, h;
React(int xx, int yy, int ww, int hh) {
this.x = xx;
this.y = yy;
this.w = ww;
this.h = hh;
}
}
class Point {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
boolean isCollision(React react) {
return react.x <= x && x <= react.x + react.w &&
react.y <= y && y <= react.y + react.h;
}
}50分写法
package _02_基础算法._01_模拟._01_P1003铺地毯;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
QuartTree qt = new QuartTree(0, 0, 150000, 150000);
for (int i = 1; i <= N; i++) {
React react = new React(sc.nextInt(), sc.nextInt(), sc.nextInt(), sc.nextInt());
react.setVal(i);
qt.add(react);
}
Point point = new Point(sc.nextInt(), sc.nextInt());
Set<React> reacts = qt.find(point);
int res = -1;
for (React react : reacts) {
if (react.val > res) {
res = react.val;
}
}
System.out.println(res);
}
}
class React {
int val;
int x, y, w, h;
React(int xx, int yy, int ww, int hh) {
this.x = xx;
this.y = yy;
this.w = ww;
this.h = hh;
}
public void setVal(int val) {
this.val = val;
}
}
class Point {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
boolean isCollision(React react) {
return react.x <= x && x <= react.x + react.w &&
react.y <= y && y <= react.y + react.h;
}
}
class QuartTree extends React {
Set<React> reacts = new HashSet<>();
QuartTree leftTop;
QuartTree leftBot;
QuartTree righTop;
QuartTree righBot;
int val;
QuartTree(int xx, int yy, int ww, int hh) {
super(xx, yy, ww, hh);
}
void add(React react) {
if (react.x + react.w < x + w / 2 &&
react.y + react.h < y + h / 2) {
// 左上角
if (leftTop == null) {
leftTop = new QuartTree(x, y, w / 2, h / 2);
}
leftTop.add(react);
} else if (react.x > x + w / 2 &&
react.y > y + h / 2) {
// 右下角
if (righBot == null) {
righBot = new QuartTree(x + w / 2, y + h / 2, w / 2, h / 2);
}
righBot.add(react);
} else if (react.x + react.w < x + w / 2 &&
react.y > y + h / 2) {
// 左下角
if (leftBot == null) {
leftBot = new QuartTree(x, y + h / 2, w / 2, h / 2);
}
leftBot.add(react);
} else if (react.x > x + w / 2 &&
react.y + react.h < y + h / 2) {
// 右上角
if (righTop == null) {
righTop = new QuartTree(x + w / 2, y, w / 2, h / 2);
}
leftTop.add(react);
} else {
reacts.add(react);
}
}
Set<React> find(Point point) {
if (point.isCollision(this)) {
Set<React> result = new HashSet<>();
for (React react : reacts) {
if (point.isCollision(react)) {
result.add(react);
}
}
if (leftTop != null &&
point.x < x + w / 2 &&
point.y < y + h / 2) {
result.addAll(leftTop.find(point));
} else if (righBot != null &&
point.x > x + w / 2 &&
point.y > y + h / 2) {
result.addAll(righBot.find(point));
} else if (leftBot != null &&
point.x < x + w / 2 &&
point.y > y + h / 2) {
result.addAll(leftBot.find(point));
} else if (righTop != null &&
point.x > x + w / 2 &&
point.y < y + h / 2) {
result.addAll(righTop.find(point));
}
return result;
} else
return null;
}
}多项式输出
# [NOIP2009 普及组] 多项式输出
## 题目描述
一元 $n$ 次多项式可用如下的表达式表示:
$$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0,a_n\ne 0$$
其中,$a_ix^i$ 称为 $i$ 次项,$a_i$ 称为 $i$ 次项的系数。给出一个一元多项式各项的次数和系数,请按照如下规定的格式要求输出该多项式:
1. 多项式中自变量为 $x$,从左到右按照次数递减顺序给出多项式。
2. 多项式中只包含系数不为 $0$ 的项。
3. 如果多项式 $n$ 次项系数为正,则多项式开头不出 `+` 号,如果多项式 $n$ 次项系数为负,则多项式以 `-` 号开头。
4. 对于不是最高次的项,以 `+` 号或者 `-` 号连接此项与前一项,分别表示此项系数为正或者系数为负。紧跟一个正整数,表示此项系数的绝对值(如果一个高于 $0$ 次的项,其系数的绝对值为 $1$,则无需输出 $1$)。如果 $x$ 的指数大于 $1$,则接下来紧跟的指数部分的形式为“$x^b$”,其中 $b$ 为 $x$ 的指数;如果 $x$ 的指数为 $1$,则接下来紧跟的指数部分形式为 $x$;如果 $x$ 的指数为 $0$,则仅需输出系数即可。
5. 多项式中,多项式的开头、结尾不含多余的空格。
## 输入格式
输入共有 $2$ 行
第一行 $1$ 个整数,$n$,表示一元多项式的次数。
第二行有 $n+1$ 个整数,其中第 $i$ 个整数表示第 $n-i+1$ 次项的系数,每两个整数之间用空格隔开。
## 输出格式
输出共 $1$ 行,按题目所述格式输出多项式。
## 样例 #1
### 样例输入 #1
```
5
100 -1 1 -3 0 10
```
### 样例输出 #1
```
100x^5-x^4+x^3-3x^2+10
```
## 样例 #2
### 样例输入 #2
```
3
-50 0 0 1
```
### 样例输出 #2
```
-50x^3+1
```
## 提示
NOIP 2009 普及组 第一题
对于100%数据,$0 \le n \le 100$,$-100 \le $系数$ \le 100$
---
$\text{upd 2022.8.1}$:新增加一组 Hack 数据。package _02_基础算法._01_模拟._02_P1067_多项式输出;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] factors = new int[N + 1];
for (int i = 0; i < factors.length; i++) {
factors[i] = sc.nextInt();
}
StringBuilder sb = new StringBuilder();
for (int i = 0, exp = N; i < factors.length; i++, exp--) {
Integer num = factors[i];
if (num != 0) {
// +
if (i != 0 && num > 0) {
sb.append("+");
}
// -
if (num < 0) {
sb.append("-");
}
// num
if (exp != 0 && Math.abs(num) != 1 || exp == 0) {
sb.append(Math.abs(num));
}
// x^?
if (exp == 0) {
;
} else if (exp == 1)
sb.append('x');
else {
sb.append("x^" + exp);
}
}
}
if (sb.length() == 0) {
sb.append("0");
}
System.out.print(sb.toString());
}
}生活大爆炸版石头剪刀布
# [NOIP2014 提高组] 生活大爆炸版石头剪刀布
## 题目描述
石头剪刀布是常见的猜拳游戏:石头胜剪刀,剪刀胜布,布胜石头。如果两个人出拳一样,则不分胜负。在《生活大爆炸》第二季第 8 集中出现了一种石头剪刀布的升级版游戏。
升级版游戏在传统的石头剪刀布游戏的基础上,增加了两个新手势:
斯波克:《星际迷航》主角之一。
蜥蜴人:《星际迷航》中的反面角色。
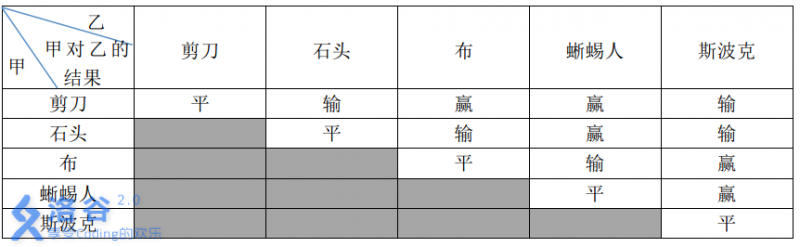
这五种手势的胜负关系如表一所示,表中列出的是甲对乙的游戏结果。
现在,小 A 和小 B 尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的,但周期长度不一定相等。例如:如果小 A 以“石头-布-石头-剪刀-蜥蜴人-斯波克”长度为 $6$ 的周期出拳,那么他的出拳序列就是“石头-布-石头-剪刀-蜥蜴人-斯波克-石头-布-石头-剪刀-蜥蜴人-斯波克-......”,而如果小 B 以“剪刀-石头-布-斯波克-蜥蜴人”长度为 $5$ 的周期出拳,那么他出拳的序列就是“剪刀-石头-布-斯波克-蜥蜴人-剪刀-石头-布-斯波克-蜥蜴人-......”
已知小 A 和小 B 一共进行 $N$ 次猜拳。每一次赢的人得 $1$ 分,输的得 $0$ 分;平局两人都得 $0$ 分。现请你统计 $N$ 次猜拳结束之后两人的得分。
## 输入格式
第一行包含三个整数:$N,N_A,N_B$,分别表示共进行 $N$ 次猜拳、小 A 出拳的周期长度,小 B 出拳的周期长度。数与数之间以一个空格分隔。
第二行包含 $N_A$ 个整数,表示小 A 出拳的规律,第三行包含 $N_B$ 个整数,表示小 B 出拳的规律。其中,$0$ 表示“剪刀”,$1$ 表示“石头”,$2$ 表示“布”,$3$ 表示“蜥蜴人”,$4 $表示“斯波克”。数与数之间以一个空格分隔。
## 输出格式
输出一行,包含两个整数,以一个空格分隔,分别表示小 A、小 B 的得分。
## 样例 #1
### 样例输入 #1
```
10 5 6
0 1 2 3 4
0 3 4 2 1 0
```
### 样例输出 #1
```
6 2
```
## 样例 #2
### 样例输入 #2
```
9 5 5
0 1 2 3 4
1 0 3 2 4
```
### 样例输出 #2
```
4 4
```
## 提示
对于$100\%$的数据,$0 < N \leq 200, 0 < N_A \leq 200, 0 < N_B \leq 200$ 。package _02_基础算法._01_模拟._03_P1328_生活大爆炸版石头剪刀布;
import java.io.BufferedInputStream;
import java.util.Scanner;
public class Main {
static int[][] map = new int[][] {
{ +0, -1, +1, +1, -1 },
{ +1, +0, -1, +1, -1 },
{ -1, +1, +0, -1, +1 },
{ -1, -1, +1, +0, +1 },
{ +1, +1, -1, -1, +0 }
};
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int Na = sc.nextInt();
int Nb = sc.nextInt();
int[] playerA = new int[Na];
int[] playerB = new int[Nb];
for (int i = 0; i < playerA.length; i++) {
playerA[i] = sc.nextInt();
}
for (int i = 0; i < playerB.length; i++) {
playerB[i] = sc.nextInt();
}
int t = 0, a = 0, b = 0;
int scoreA = 0, scoreB = 0;
while (t < N) {
scoreA += map[playerA[a]][playerB[b]] == 1 ? 1 : 0;// map[i][j] 存的是i对j的结果
scoreB += map[playerB[b]][playerA[a]] == 1 ? 1 : 0;
a=++a%playerA.length;// 循环
b=++b%playerB.length;// 循环
t++;
}
System.out.println(scoreA + " " + scoreB);
}
}玩具谜题
# [NOIP2016 提高组] 玩具谜题
## 题目背景
NOIP2016 提高组 D1T1
## 题目描述
小南有一套可爱的玩具小人, 它们各有不同的职业。
有一天, 这些玩具小人把小南的眼镜藏了起来。 小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:
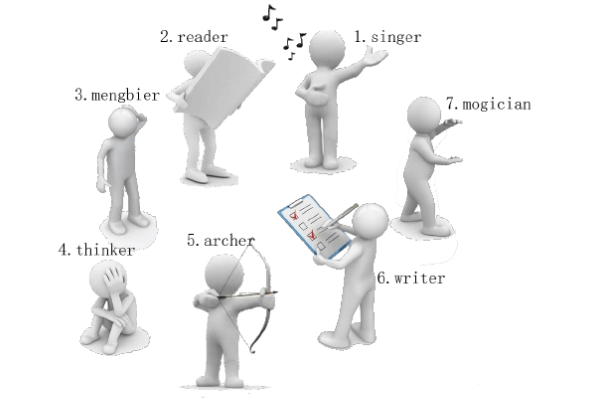
这时 singer 告诉小南一个谜題: “眼镜藏在我左数第 $3$ 个玩具小人的右数第 $1$ 个玩具小人的左数第 $2$ 个玩具小人那里。 ”
小南发现, 这个谜题中玩具小人的朝向非常关键, 因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人, 它的左边是顺时针方向, 右边是逆时针方向; 而面向圈外的玩具小人, 它的左边是逆时针方向, 右边是顺时针方向。
小南一边艰难地辨认着玩具小人, 一边数着:
singer 朝内, 左数第 $3$ 个是 archer。
archer 朝外,右数第 $1$ 个是 thinker 。
thinker 朝外, 左数第 $2$ 个是 writer。
所以眼镜藏在 writer 这里!
虽然成功找回了眼镜, 但小南并没有放心。 如果下次有更多的玩具小人藏他的眼镜, 或是谜题的长度更长, 他可能就无法找到眼镜了。所以小南希望你写程序帮他解决类似的谜题。 这样的谜題具体可以描述为:
有 $n$ 个玩具小人围成一圈, 已知它们的职业和朝向。现在第 $1$ 个玩具小人告诉小南一个包含 $m$ 条指令的谜題, 其中第 $z$ 条指令形如“左数/右数第 $s$,个玩具小人”。 你需要输出依次数完这些指令后,到达的玩具小人的职业。
## 输入格式
输入的第一行包含两个正整数 $n,m$,表示玩具小人的个数和指令的条数。
接下来 $n$ 行,每行包含一个整数和一个字符串,以逆时针为顺序给出每个玩具小人的朝向和职业。其中 $0$ 表示朝向圈内,$1$ 表示朝向圈外。 保证不会出现其他的数。字符串长度不超过 $10$ 且仅由小写字母构成,字符串不为空,并且字符串两两不同。整数和字符串之间用一个空格隔开。
接下来 $m$ 行,其中第 $i$ 行包含两个整数 $a_i,s_i$,表示第 $i$ 条指令。若 $a_i=0$,表示向左数 $s_i$ 个人;若 $a_i=1$,表示向右数 $s_i$ 个人。 保证 $a_i$ 不会出现其他的数,$1 \le s_i < n$。
## 输出格式
输出一个字符串,表示从第一个读入的小人开始,依次数完 $m$ 条指令后到达的小人的职业。
## 样例 #1
### 样例输入 #1
```
7 3
0 singer
0 reader
0 mengbier
1 thinker
1 archer
0 writer
1 mogician
0 3
1 1
0 2
```
### 样例输出 #1
```
writer
```
## 样例 #2
### 样例输入 #2
```
10 10
1 C
0 r
0 P
1 d
1 e
1 m
1 t
1 y
1 u
0 V
1 7
1 1
1 4
0 5
0 3
0 1
1 6
1 2
0 8
0 4
```
### 样例输出 #2
```
y
```
## 提示
【样例1说明】
这组数据就是【题目描述】 中提到的例子。
【子任务】
子任务会给出部分测试数据的特点。 如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
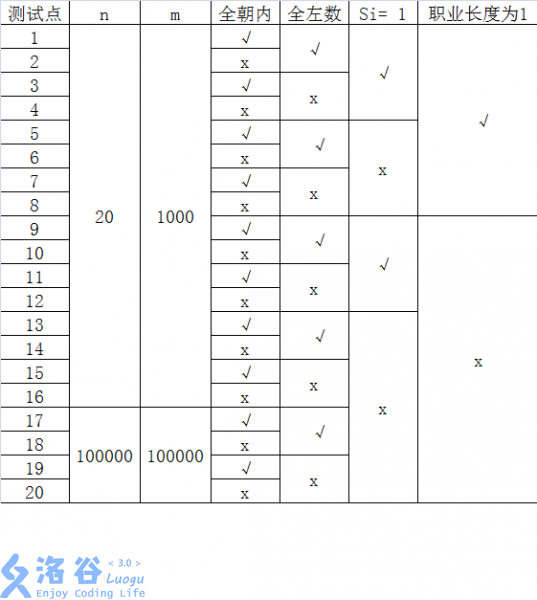
其中一些简写的列意义如下:
- 全朝内: 若为“√”, 表示该测试点保证所有的玩具小人都朝向圈内;
- 全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的 $1\leq z\leq m, a_i=0$;
- $s=1$:若为“√”,表示该测试点保证所有的指令都只数 $1$ 个,即对任意的 $1\leq z\leq m,s_i=1$;
职业长度为 $1$:若为“√”,表示该测试点保证所有玩具小人的职业一定是一个长度为$1$的字符串。package _02_基础算法._01_模拟._04_玩具谜题;
import java.io.BufferedInputStream;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int M = sc.nextInt();
int[] direction = new int[N];
String[] names = new String[N];
for (int i = 0; i < N; i++) {
direction[i] = sc.nextInt() == 0 ? 1 : -1;// 朝内为1,朝外为-1
names[i] = sc.next();
}
int pos = 0;
for (int i = 0; i < M; i++) {
int right = sc.nextInt() == 1 ? 1 : -1;// 右手边为1 左手边为-1
int cnt = sc.nextInt();
// 从当前位置偏移多少位置,根据图来看,小人面朝内(+1)且往右手(+1)方向数一个位置(+1),就是下一个位置。,就是 +1 x +1 x +1;
int offset = direction[pos] * right * cnt;
pos += offset;
pos %= direction.length;
if (pos < 0) {
pos = direction.length + pos;
}
}
System.out.println(names[pos]);
}
}乒乓球
# [NOIP2003 普及组] 乒乓球
## 题目背景
国际乒联现在主席沙拉拉自从上任以来就立志于推行一系列改革,以推动乒乓球运动在全球的普及。其中 $11$ 分制改革引起了很大的争议,有一部分球员因为无法适应新规则只能选择退役。华华就是其中一位,他退役之后走上了乒乓球研究工作,意图弄明白 $11$ 分制和 $21$ 分制对选手的不同影响。在开展他的研究之前,他首先需要对他多年比赛的统计数据进行一些分析,所以需要你的帮忙。
## 题目描述
华华通过以下方式进行分析,首先将比赛每个球的胜负列成一张表,然后分别计算在 $11$ 分制和 $21$ 分制下,双方的比赛结果(截至记录末尾)。
比如现在有这么一份记录,(其中 $\texttt W$ 表示华华获得一分,$\texttt L$ 表示华华对手获得一分):
$\texttt{WWWWWWWWWWWWWWWWWWWWWWLW}$
在 $11$ 分制下,此时比赛的结果是华华第一局 $11$ 比 $0$ 获胜,第二局 $11$ 比 $0$ 获胜,正在进行第三局,当前比分 $1$ 比 $1$。而在 $21$ 分制下,此时比赛结果是华华第一局 $21$ 比 $0$ 获胜,正在进行第二局,比分 $2$ 比 $1$。如果一局比赛刚开始,则此时比分为 $0$ 比 $0$。直到分差大于或者等于 $2$,才一局结束。
你的程序就是要对于一系列比赛信息的输入($\texttt{WL}$ 形式),输出正确的结果。
## 输入格式
每个输入文件包含若干行字符串,字符串有大写的 $\texttt W$ 、 $\texttt L$ 和 $\texttt E$ 组成。其中 $\texttt E$ 表示比赛信息结束,程序应该忽略 $\texttt E$ 之后的所有内容。
## 输出格式
输出由两部分组成,每部分有若干行,每一行对应一局比赛的比分(按比赛信息输入顺序)。其中第一部分是 $11$ 分制下的结果,第二部分是 $21$ 分制下的结果,两部分之间由一个空行分隔。
## 样例 #1
### 样例输入 #1
```
WWWWWWWWWWWWWWWWWWWW
WWLWE
```
### 样例输出 #1
```
11:0
11:0
1:1
21:0
2:1
```
## 提示
每行至多 $25$ 个字母,最多有 $2500$ 行。
(注:事实上有一个测试点有 $2501$ 行数据。)
**【题目来源】**
NOIP 2003 普及组第一题package _02_基础算法._01_模拟._05_P1042_乒乓球;
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
LinkedList<Record> records_11 = new LinkedList<>();
LinkedList<Record> records_21 = new LinkedList<>();
outer: while (sc.hasNext()) {
String line = sc.nextLine();
for (char ch : line.toCharArray()) {
Record record_11 = records_11.size() >= 1 ? records_11.getLast() : null;
Record record_21 = records_21.size() >= 1 ? records_21.getLast() : null;
// 必须一个人的分数达到11分并且分数之差大于2
if (record_11 == null || (record_11.a >= 11 || record_11.b >= 11) && Math.abs(record_11.a - record_11.b) >= 2) {
records_11.addLast(record_11 = new Record(0, 0));
}
// 必须一个人的分数达到21分并且分数之差大于2
if (record_21 == null || (record_21.a >= 21 || record_21.b >= 21) && Math.abs(record_21.a - record_21.b) >= 2) {
records_21.addLast(record_21 = new Record(0, 0));
}
switch (ch) {
case 'W':
record_11.a++;
record_21.a++;
break;
case 'L':
record_11.b++;
record_21.b++;
break;
case 'E':
break outer;
}
}
}
for (Record record : records_11) {
System.out.println(record.a + ":" + record.b);
}
System.out.println("");// 换行
for (Record record : records_21) {
System.out.println(record.a + ":" + record.b);
}
}
}
class Record {
int a, b;
Record(int aa, int bb) {
a = aa;
b = bb;
}
}数字统计
# [NOIP2010 普及组] 数字统计
## 题目描述
请统计某个给定范围$[L, R]$的所有整数中,数字 $2$ 出现的次数。
比如给定范围$[2, 22]$,数字$ 2$ 在数 $2 $中出现了 $1$ 次,在数$ 12$ 中出现 $1$ 次,在数 $20$ 中出现 $1 $次,在数 21 中出现 $1$ 次,在数 $22$ 中出现 $2 $次,所以数字$ 2$ 在该范围内一共出现了 $6$次。
## 输入格式
$2$个正整数 $L$ 和 $R$,之间用一个空格隔开。
## 输出格式
数字 $2 $出现的次数。
## 样例 #1
### 样例输入 #1
```
2 22
```
### 样例输出 #1
```
6
```
## 样例 #2
### 样例输入 #2
```
2 100
```
### 样例输出 #2
```
20
```
## 提示
$1 ≤ L ≤R≤ 100000$。package _02_基础算法._01_模拟._06_P1179_数字统计;
import java.io.BufferedInputStream;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int start = sc.nextInt();
int ended = sc.nextInt();
int cnt = 0;
for (int i = start; i <= ended; i++) {
cnt += counter(i + "");
}
System.out.println(cnt);
}
static int counter(String str) {
int res = 0;
for (char ch : str.toCharArray()) {
if (ch == '2')
res++;
}
return res;
}
}神奇的幻方
# [NOIP2015 提高组] 神奇的幻方
## 题目描述
幻方是一种很神奇的 $N\times N$ 矩阵:它由数字 $1,2,3,\cdots \cdots ,N \times N$ 构成,且每行、每列及两条对角线上的数字之和都相同。
当 $N$ 为奇数时,我们可以通过下方法构建一个幻方:
首先将 $1$ 写在第一行的中间。
之后,按如下方式从小到大依次填写每个数 $K (K=2,3,\cdots,N \times N)$ :
1. 若 $(K-1)$ 在第一行但不在最后一列,则将 $K$ 填在最后一行, $(K-1)$ 所在列的右一列;
2. 若 $(K-1)$ 在最后一列但不在第一行,则将 $K$ 填在第一列, $(K-1)$ 所在行的上一行;
3. 若 $(K-1)$ 在第一行最后一列,则将 $K$ 填在 $(K-1)$ 的正下方;
4. 若 $(K-1)$ 既不在第一行,也不在最后一列,如果 $(K-1)$ 的右上方还未填数,则将 $K$ 填在 $(K-1)$ 的右上方,否则将 $K$ 填在 $(K-1)$ 的正下方。
现给定 $N$ ,请按上述方法构造 $N \times N$ 的幻方。
## 输入格式
一个正整数 $N$,即幻方的大小。
## 输出格式
共 $N$ 行,每行 $N$ 个整数,即按上述方法构造出的 $N \times N$ 的幻方,相邻两个整数之间用单空格隔开。
## 样例 #1
### 样例输入 #1
```
3
```
### 样例输出 #1
```
8 1 6
3 5 7
4 9 2
```
## 样例 #2
### 样例输入 #2
```
25
```
### 样例输出 #2
```
327 354 381 408 435 462 489 516 543 570 597 624 1 28 55 82 109 136 163 190 217 244 271 298 325
353 380 407 434 461 488 515 542 569 596 623 25 27 54 81 108 135 162 189 216 243 270 297 324 326
379 406 433 460 487 514 541 568 595 622 24 26 53 80 107 134 161 188 215 242 269 296 323 350 352
405 432 459 486 513 540 567 594 621 23 50 52 79 106 133 160 187 214 241 268 295 322 349 351 378
431 458 485 512 539 566 593 620 22 49 51 78 105 132 159 186 213 240 267 294 321 348 375 377 404
457 484 511 538 565 592 619 21 48 75 77 104 131 158 185 212 239 266 293 320 347 374 376 403 430
483 510 537 564 591 618 20 47 74 76 103 130 157 184 211 238 265 292 319 346 373 400 402 429 456
509 536 563 590 617 19 46 73 100 102 129 156 183 210 237 264 291 318 345 372 399 401 428 455 482
535 562 589 616 18 45 72 99 101 128 155 182 209 236 263 290 317 344 371 398 425 427 454 481 508
561 588 615 17 44 71 98 125 127 154 181 208 235 262 289 316 343 370 397 424 426 453 480 507 534
587 614 16 43 70 97 124 126 153 180 207 234 261 288 315 342 369 396 423 450 452 479 506 533 560
613 15 42 69 96 123 150 152 179 206 233 260 287 314 341 368 395 422 449 451 478 505 532 559 586
14 41 68 95 122 149 151 178 205 232 259 286 313 340 367 394 421 448 475 477 504 531 558 585 612
40 67 94 121 148 175 177 204 231 258 285 312 339 366 393 420 447 474 476 503 530 557 584 611 13
66 93 120 147 174 176 203 230 257 284 311 338 365 392 419 446 473 500 502 529 556 583 610 12 39
92 119 146 173 200 202 229 256 283 310 337 364 391 418 445 472 499 501 528 555 582 609 11 38 65
118 145 172 199 201 228 255 282 309 336 363 390 417 444 471 498 525 527 554 581 608 10 37 64 91
144 171 198 225 227 254 281 308 335 362 389 416 443 470 497 524 526 553 580 607 9 36 63 90 117
170 197 224 226 253 280 307 334 361 388 415 442 469 496 523 550 552 579 606 8 35 62 89 116 143
196 223 250 252 279 306 333 360 387 414 441 468 495 522 549 551 578 605 7 34 61 88 115 142 169
222 249 251 278 305 332 359 386 413 440 467 494 521 548 575 577 604 6 33 60 87 114 141 168 195
248 275 277 304 331 358 385 412 439 466 493 520 547 574 576 603 5 32 59 86 113 140 167 194 221
274 276 303 330 357 384 411 438 465 492 519 546 573 600 602 4 31 58 85 112 139 166 193 220 247
300 302 329 356 383 410 437 464 491 518 545 572 599 601 3 30 57 84 111 138 165 192 219 246 273
301 328 355 382 409 436 463 490 517 544 571 598 625 2 29 56 83 110 137 164 191 218 245 272 299
```
## 提示
对于$100\%$的数据,对于全部数据, $1 \leq N \leq 39$ 且 $N$ 为奇数。
NOIp2015 提高组 d1t1package _02_基础算法._01_模拟._07_P2615_神奇的幻方;
import java.io.BufferedInputStream;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int[][] matrix = new int[N][N];
int preX = N / 2;
int preY = 0;
int num = 1;
matrix[preY][preX] = num++;
while (num <= N * N) {
if (preY == 0 && preX != N - 1) {
matrix[preY = N - 1][preX = preX + 1] = num++;
continue;
}
if (preX == N - 1 && preY != 0) {
matrix[preY = preY - 1][preX = 0] = num++;
continue;
}
if (preY == 0 && preX == N - 1) {
matrix[preY = preY + 1][preX] = num++;
continue;
}
if (preY != 0 && preX != N - 1) {
if (matrix[preY - 1][preX + 1] == 0) {
matrix[preY = preY - 1][preX = preX + 1] = num++;
} else {
matrix[preY = preY + 1][preX] = num++;
}
}
}
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
System.out.print(matrix[i][j]);
if (j != matrix[i].length - 1) {
System.out.print(" ");
} else {
System.out.print("\n");
}
}
}
}
}Part 2.2 排序算法
- P1177 【模板】快速排序
- P1059 明明的随机数
- P1068 分数线划定
- P1051 谁拿了最多奖学金
- P1309 瑞士轮
- P1908 逆序对
模板快速排序
# 【模板】快速排序
## 题目描述
利用快速排序算法将读入的 $N$ 个数从小到大排序后输出。
快速排序是信息学竞赛的必备算法之一。对于快速排序不是很了解的同学可以自行上网查询相关资料,掌握后独立完成。(C++ 选手请不要试图使用 `STL`,虽然你可以使用 `sort` 一遍过,但是你并没有掌握快速排序算法的精髓。)
## 输入格式
第 $1$ 行为一个正整数 $N$,第 $2$ 行包含 $N$ 个空格隔开的正整数 $a_i$,为你需要进行排序的数,数据保证了 $a_i$ 不超过 $10^9$。
## 输出格式
将给定的 $N$ 个数从小到大输出,数之间空格隔开,行末换行且无空格。
## 样例 #1
### 样例输入 #1
```
5
4 2 4 5 1
```
### 样例输出 #1
```
1 2 4 4 5
```
## 提示
对于 $20\%$ 的数据,有 $N\leq 10^3$;
对于 $100\%$ 的数据,有 $N\leq 10^5$。package _02_基础算法._02_排序算法._01_P1177_模板_快速排序;
import java.io.BufferedInputStream;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int[] data = new int[N];
for (int i = 0; i < data.length; i++) {
data[i] = sc.nextInt();
}
quickSort(data);
for (int i = 0; i < data.length; i++) {
System.out.print(data[i]);
if (i != data.length - 1)
System.out.print(" ");
else
System.out.println("");
}
}
static void quickSort(int[] arr) {
process(arr, 0, arr.length - 1);
}
static void process(int[] arr, int left, int right) {
if (left < right) {
int k = left + (int) (Math.random() * (right - left));
int midVal = arr[k];
int L = left, R = right;
int cur = left;
while (cur <= right && L <= R) {
if (arr[cur] < midVal) {
exchange(arr, cur++, L++);
} else if (arr[cur] > midVal) {
exchange(arr, cur, R--);// 需要思考为什么这里不用写 cur++;
} else if (arr[cur] == midVal) {
cur++;
}
}
process(arr, left, L - 1);
process(arr, R + 1, right);
}
}
static void exchange(int[] arr, int i, int j) {
if (i != j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
}明明的随机数
# [NOIP2006 普及组] 明明的随机数
## 题目描述
明明想在学校中请一些同学一起做一项问卷调查,为了实验的客观性,他先用计算机生成了 $N$ 个 $1$ 到 $1000$ 之间的随机整数 $(N\leq100)$,对于其中重复的数字,只保留一个,把其余相同的数去掉,不同的数对应着不同的学生的学号。然后再把这些数从小到大排序,按照排好的顺序去找同学做调查。请你协助明明完成“去重”与“排序”的工作。
## 输入格式
输入有两行,第 $1$ 行为 $1$ 个正整数,表示所生成的随机数的个数 $N$。
第 $2$ 行有 $N$ 个用空格隔开的正整数,为所产生的随机数。
## 输出格式
输出也是两行,第 $1$ 行为 $1$ 个正整数 $M$,表示不相同的随机数的个数。
第 $2$ 行为 $M$ 个用空格隔开的正整数,为从小到大排好序的不相同的随机数。
## 样例 #1
### 样例输入 #1
```
10
20 40 32 67 40 20 89 300 400 15
```
### 样例输出 #1
```
8
15 20 32 40 67 89 300 400
```
## 提示
NOIP 2006 普及组 第一题package _02_基础算法._02_排序算法._02_P1059_明明的随机数;
import java.io.BufferedInputStream;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int[] arr = new int[N];
for (int i = 0; i < arr.length; i++) {
arr[i] = sc.nextInt();
}
Arrays.sort(arr);
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
if (i + 1 < arr.length && arr[i] == arr[i + 1]) {
continue;
} else {
list.add(arr[i]);
}
}
System.out.println(list.size());
for (Integer num : list) {
System.out.print(num + " ");
}
}
}分数线划定
# [NOIP2009 普及组] 分数线划定
## 题目描述
世博会志愿者的选拔工作正在 A 市如火如荼的进行。为了选拔最合适的人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。面试分数线根据计划录取人数的 $150\%$ 划定,即如果计划录取 $m$ 名志愿者,则面试分数线为排名第 $m \times 150\%$(向下取整)名的选手的分数,而最终进入面试的选手为笔试成绩不低于面试分数线的所有选手。
现在就请你编写程序划定面试分数线,并输出所有进入面试的选手的报名号和笔试成绩。
## 输入格式
第一行,两个整数 $n,m(5 \leq n \leq 5000,3 \leq m \leq n)$,中间用一个空格隔开,其中 $n$ 表示报名参加笔试的选手总数,$m$ 表示计划录取的志愿者人数。输入数据保证 $m \times 150\%$ 向下取整后小于等于 $n$。
第二行到第 $n+1$ 行,每行包括两个整数,中间用一个空格隔开,分别是选手的报名号 $k(1000 \leq k \leq 9999)$和该选手的笔试成绩 $s(1 \leq s \leq 100)$。数据保证选手的报名号各不相同。
## 输出格式
第一行,有 $2$ 个整数,用一个空格隔开,第一个整数表示面试分数线;第二个整数为进入面试的选手的实际人数。
从第二行开始,每行包含 $2$ 个整数,中间用一个空格隔开,分别表示进入面试的选手的报名号和笔试成绩,按照笔试成绩从高到低输出,如果成绩相同,则按报名号由小到大的顺序输出。
## 样例 #1
### 样例输入 #1
```
6 3
1000 90
3239 88
2390 95
7231 84
1005 95
1001 88
```
### 样例输出 #1
```
88 5
1005 95
2390 95
1000 90
1001 88
3239 88
```
## 提示
【样例说明】
$m \times 150\% = 3 \times150\% = 4.5$,向下取整后为 $4$。保证 $4$ 个人进入面试的分数线为 $88$,但因为 $88$ 有重分,所以所有成绩大于等于 $88$ 的选手都可以进入面试,故最终有 $5$ 个人进入面试。
NOIP 2009 普及组 第二题package _02_基础算法._02_排序算法._03_P1068_分数线划定;
import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int M = sc.nextInt();
Item[] list = new Item[N];
for (int i = 0; i < N; i++) {
list[i] = new Item(sc.nextInt(), sc.nextInt());
}
// java默认排序算法具有有稳定性,先按id升序排序,再按分数升序排序即可
Arrays.sort(list, (o1, o2) -> Integer.compare(o1.id, o2.id));
Arrays.sort(list, (o1, o2) -> -Integer.compare(o1.score, o2.score));
int k = (int) (M * 1.5);// 计算面试人数
k = k >= N ? N : k;// 防止越界
while (k < N/* 防止越界 */ && list[k - 1].score == list[k].score/* 同分判断 */)
k++;// 跳过同分
System.out.println(list[k - 1].score + " " + (k));
for (int i = 0; i < k; i++) {
System.out.println(list[i].id + " " + list[i].score);
}
}
}
class Item {
int id, score;
public Item(int id, int score) {
this.id = id;
this.score = score;
}
}谁拿了最多奖学金
# [NOIP2005 提高组] 谁拿了最多奖学金
## 题目描述
某校的惯例是在每学期的期末考试之后发放奖学金。发放的奖学金共有五种,获取的条件各自不同:
1. 院士奖学金,每人 $8000$ 元,期末平均成绩高于 $80$ 分($>80$),并且在本学期内发表$1$篇或$1$篇以上论文的学生均可获得;
2. 五四奖学金,每人 $4000$ 元,期末平均成绩高于 $85$ 分($>85$),并且班级评议成绩高于 $80$ 分($>80$)的学生均可获得;
3. 成绩优秀奖,每人 $2000$ 元,期末平均成绩高于 $90$ 分($>90$)的学生均可获得;
4. 西部奖学金,每人 $1000$ 元,期末平均成绩高于 $85$ 分($>85$)的西部省份学生均可获得;
5. 班级贡献奖,每人 $850$ 元,班级评议成绩高于 $80$ 分($>80$)的学生干部均可获得;
只要符合条件就可以得奖,每项奖学金的获奖人数没有限制,每名学生也可以同时获得多项奖学金。例如姚林的期末平均成绩是 $87$ 分,班级评议成绩 $82$ 分,同时他还是一位学生干部,那么他可以同时获得五四奖学金和班级贡献奖,奖金总数是 $4850$ 元。
现在给出若干学生的相关数据,请计算哪些同学获得的奖金总数最高(假设总有同学能满足获得奖学金的条件)。
## 输入格式
第一行是$1$个整数 $N$,表示学生的总数。
接下来的 $N$ 行每行是一位学生的数据,从左向右依次是姓名,期末平均成绩,班级评议成绩,是否是学生干部,是否是西部省份学生,以及发表的论文数。姓名是由大小写英文字母组成的长度不超过 $20$ 的字符串(不含空格);期末平均成绩和班级评议成绩都是 $0$ 到 $100$ 之间的整数(包括 $0$ 和 $100$);是否是学生干部和是否是西部省份学生分别用 $1$ 个字符表示,$\tt Y$ 表示是,$\tt N$ 表示不是;发表的论文数是 $0$ 到 $10$ 的整数(包括 $0$ 和 $10$)。每两个相邻数据项之间用一个空格分隔。
## 输出格式
共 $3$ 行。
- 第 $1$ 行是获得最多奖金的学生的姓名。
- 第 $2$ 行是这名学生获得的奖金总数。如果有两位或两位以上的学生获得的奖金最多,输出他们之中在输入文件中出现最早的学生的姓名。
- 第 $3$ 行是这 $N$ 个学生获得的奖学金的总数。
## 样例 #1
### 样例输入 #1
```
4
YaoLin 87 82 Y N 0
ChenRuiyi 88 78 N Y 1
LiXin 92 88 N N 0
ZhangQin 83 87 Y N 1
```
### 样例输出 #1
```
ChenRuiyi
9000
28700
```
## 提示
**【数据范围】**
对于 $100\%$ 的数据,满足 $1 \le N \le 100$。
**【题目来源】**
NOIP 2005 提高组第一题package _02_基础算法._02_排序算法._04_P1051_谁拿了最多奖学金;
import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
sc.nextLine();
Item[] items = new Item[N];
int sum = 0;
for (int i = 0; i < items.length; i++) {
int val = 0;
String[] infos = sc.nextLine().split(" ");
String name = infos[0];
int qi_mo = Integer.valueOf(infos[1]);
int class_score = Integer.valueOf(infos[2]);
boolean isXue = "Y".equals(infos[3]) ? true : false;
boolean isXi = "Y".equals(infos[4]) ? true : false;
int articles_cnt = Integer.valueOf(infos[5]);
if (qi_mo > 80 && articles_cnt >= 1)
val += 8000;
if (qi_mo > 85 && class_score > 80)
val += 4000;
if (qi_mo > 90)
val += 2000;
if (isXi && qi_mo > 85)
val += 1000;
if (isXue && class_score > 80)
val += 850;
sum += val;
items[i] = new Item(name, val);
}
Arrays.sort(items, (o1, o2) -> -Integer.compare(o1.val, o2.val));
System.out.println(items[0].name);
System.out.println(items[0].val);
System.out.println(sum);
}
}
class Item {
String name;
int val;
public Item(String name, int val) {
this.name = name;
this.val = val;
}
}瑞士轮
# [NOIP2011 普及组] 瑞士轮
## 题目背景
在双人对决的竞技性比赛,如乒乓球、羽毛球、国际象棋中,最常见的赛制是淘汰赛和循环赛。前者的特点是比赛场数少,每场都紧张刺激,但偶然性较高。后者的特点是较为公平,偶然性较低,但比赛过程往往十分冗长。
本题中介绍的瑞士轮赛制,因最早使用于$1895$年在瑞士举办的国际象棋比赛而得名。它可以看作是淘汰赛与循环赛的折中,既保证了比赛的稳定性,又能使赛程不至于过长。
## 题目描述
$2 \times N$ 名编号为 $1\sim 2N$ 的选手共进行R 轮比赛。每轮比赛开始前,以及所有比赛结束后,都会按照总分从高到低对选手进行一次排名。选手的总分为第一轮开始前的初始分数加上已参加过的所有比赛的得分和。总分相同的,约定编号较小的选手排名靠前。
每轮比赛的对阵安排与该轮比赛开始前的排名有关:第$1$ 名和第$2$ 名、第 $3$ 名和第 $4$名、……、第$2K - 1 $名和第$ 2K$名、…… 、第$2N - 1 $名和第$2N$名,各进行一场比赛。每场比赛胜者得$1 $分,负者得 $0 $分。也就是说除了首轮以外,其它轮比赛的安排均不能事先确定,而是要取决于选手在之前比赛中的表现。
现给定每个选手的初始分数及其实力值,试计算在R 轮比赛过后,排名第$ Q$ 的选手编号是多少。我们假设选手的实力值两两不同,且每场比赛中实力值较高的总能获胜。
## 输入格式
第一行是三个正整数$N,R ,Q$,每两个数之间用一个空格隔开,表示有 $2 \times N $名选手、$R$ 轮比赛,以及我们关心的名次 $Q$。
第二行是$2 \times N$ 个非负整数$s_1, s_2, …, s_{2N}$,每两个数之间用一个空格隔开,其中$ s_i $表示编号为$i$ 的选手的初始分数。 第三行是$2 \times N$ 个正整数$w_1 , w_2 , …, w_{2N}$,每两个数之间用一个空格隔开,其中 $w_i$ 表示编号为$i$ 的选手的实力值。
## 输出格式
一个整数,即$R$ 轮比赛结束后,排名第$ Q$ 的选手的编号。
## 样例 #1
### 样例输入 #1
```
2 4 2
7 6 6 7
10 5 20 15
```
### 样例输出 #1
```
1
```
## 提示
【样例解释】
【数据范围】
对于$30\% $的数据,$1 ≤ N ≤ 100$;
对于$50\% $的数据,$1 ≤ N ≤ 10,000 $;
对于$100\%$的数据,$1 ≤ N ≤ 100,000,1 ≤ R ≤ 50,1 ≤ Q ≤ 2N,0 ≤ s_1, s_2, …, s_{2N}≤10^8,1 ≤w_1, w_2 , …, w_{2N}≤ 10^8$。
noip2011普及组第3题。直观解法:TLE、严重超时
package _02_基础算法._02_排序算法._05_P1309_瑞士轮_暴力模拟;
import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int R = sc.nextInt();
int Q = sc.nextInt();
Item[] items = new Item[N * 2];
for (int idx = 0; idx < items.length; idx++) {
items[idx] = new Item(idx + 1, sc.nextInt(), 0);
}
for (int idx = 0; idx < items.length; idx++) {
items[idx].tough = sc.nextInt();
}
// 先按id升序,再按分数降序
// Arrays.sort(items, (o1, o2) -> Integer.compare(o1.id, o2.id));
// Arrays.sort(items, (o1, o2) -> -Integer.compare(o1.score, o2.score));
for (int t = 0; t < R; t++) {
for (int j = 0; j < items.length - 1; j += 2) {
if (items[j].tough > items[j + 1].tough) {
items[j].score += 1;
continue;
}
if (items[j].tough < items[j + 1].tough) {
items[j + 1].score += 1;
continue;
}
}
Arrays.sort(items, (o1, o2) -> Integer.compare(o1.id, o2.id));
Arrays.sort(items, (o1, o2) -> -Integer.compare(o1.score, o2.score));
}
System.out.println(items[Q - 1].id);
}
}
class Item {
int id, score, tough;
public Item(int id, int score, int tough) {
this.id = id;
this.score = score;
this.tough = tough;
}
}优化后解法:第一次需要排序,后序只需使用merge,时间复杂度O(n)
依然超时,但可能是java的原因,500ms对c++来说可能绰绰有余,但对java来说可能远远不够
// package _02_基础算法._02_排序算法._05_P1309_瑞士轮;
import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
String[] line0 = sc.nextLine().split(" ");
String[] line1 = sc.nextLine().split(" ");
String[] line2 = sc.nextLine().split(" ");
int N = Integer.parseInt(line0[0]);
int R = Integer.parseInt(line0[1]);
int Q = Integer.parseInt(line0[2]);
Item[] items = new Item[N * 2];
Item[] winer = new Item[N];
Item[] loser = new Item[N];
int w_len = 0;
int l_len = 0;
int w = 0, l = 0, m = 0;
for (int idx = 0; idx < items.length; idx++) {
items[idx] = new Item(
idx + 1,
Integer.parseInt(line1[idx]),
Integer.parseInt(line2[idx]));
}
// new QuickSorter<Item>().quickSort(items);
Arrays.sort(items);
for (int t = 0; t < R; t++) {
w_len = 0;
l_len = 0;
for (int n = 0; n < items.length - 1; n += 2) {
if (items[n].tough > items[n + 1].tough) {
winer[w_len++] = items[n];
loser[l_len++] = items[n + 1];
items[n].score += 1;
} else {
winer[w_len++] = items[n + 1];
loser[l_len++] = items[n];
items[n + 1].score += 1;
}
}
// merge
w = 0;
l = 0;
m = 0;
while (w < w_len && l < l_len) {
// if (winer[w].score > loser[l].score) {
// items[m++] = winer[w++];
// } else if (winer[w].score < loser[l].score) {
// items[m++] = loser[l++];
// } else {
// if (winer[w].id < loser[l].id) {
// items[m++] = winer[w++];
// } else {
// items[m++] = loser[l++];
// }
// }
if (winer[w].compareTo(loser[l]) < 0) {
items[m++] = winer[w++];
} else {
items[m++] = loser[l++];
}
}
while (w < w_len)
items[m++] = winer[w++];
while (l < l_len)
items[m++] = loser[l++];
}
System.out.println(items[Q - 1].id);
}
}
class QuickSorter<T extends Comparable<T>> {
void quickSort(T[] items) {
process(items, 0, items.length - 1);
}
void process(T[] items, int left, int right) {
if (left < right) {
T ref = items[(int) (left + Math.random() * (right - left))];
int L = left, R = right;
int cur = left;
while (cur <= right && L <= R) {
if (items[cur].compareTo(ref) < 0) {
swap(items, L++, cur++);
} else {
swap(items, R--, cur);
}
}
process(items, left, L - 1);
process(items, R + 1, right);
}
}
void swap(T[] items, int i, int j) {
if (i != j) {
T temp = items[j];
items[j] = items[i];
items[i] = temp;
}
}
}
class Item implements Comparable<Item> {
int id, score, tough;
public Item(int id, int score, int tough) {
this.id = id;
this.score = score;
this.tough = tough;
}
@Override
public int compareTo(Item other) {
int dif = -(this.score - other.score);
int res = dif != 0 ? dif : this.id - other.id;
return res;
}
@Override
public String toString() {
return "Item [id=" + id + ", score=" + score + ", tough=" + tough + "]";
}
}逆序对
# 逆序对
## 题目描述
猫猫 TOM 和小老鼠 JERRY 最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。
最近,TOM 老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中 $a_i>a_j$ 且 $i<j$ 的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。
**Update:数据已加强。**
## 输入格式
第一行,一个数 $n$,表示序列中有 $n$个数。
第二行 $n$ 个数,表示给定的序列。序列中每个数字不超过 $10^9$。
## 输出格式
输出序列中逆序对的数目。
## 样例 #1
### 样例输入 #1
```
6
5 4 2 6 3 1
```
### 样例输出 #1
```
11
```
## 提示
对于 $25\%$ 的数据,$n \leq 2500$
对于 $50\%$ 的数据,$n \leq 4 \times 10^4$。
对于所有数据,$n \leq 5 \times 10^5$
请使用较快的输入输出
应该不会 $O(n^2)$ 过 50 万吧 by chen_zhepackage _02_基础算法._02_排序算法._06_P1908_逆序对;
import java.io.BufferedInputStream;
//import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int N = sc.nextInt();
int[] nums = new int[N];
for (int i = 0; i < nums.length; i++) {
nums[i] = sc.nextInt();
}
mergeSort(nums);
// System.out.println(Arrays.toString(nums));
System.out.println(ans);
}
static long ans = 0;
static void mergeSort(int[] arr) {
process(arr, 0, arr.length - 1);
}
static void process(int[] arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
process(arr, left, mid);
process(arr, mid + 1, right);
merge(arr, left, mid, mid + 1, right);
}
}
static void merge(int[] arr, int L1_start, int L1_end, int L2_start, int L2_end) {
int[] help = new int[L2_end - L1_start + 1];
int N = 0, l1 = L1_start, l2 = L2_start;
while (l1 <= L1_end && l2 <= L2_end) {
if (arr[l1] > arr[l2]) {
// System.out.println(arr[l1]+" "+arr[l2]);
ans += L1_end - l1 + 1;
}
help[N++] = arr[l1] > arr[l2] ? arr[l2++] : arr[l1++];
}
while (l1 <= L1_end) {
help[N++] = arr[l1++];
}
while (l2 <= L2_end) {
help[N++] = arr[l2++];
}
N = 0;
while (N < help.length) {
arr[L1_start + N] = help[N];
N++;
}
}
}Part 2.3 二分答案
对一个满足单调性质的问题,我们可以采用二分答案的方法来解决。
- P1024 一元三次方程求解
- P2678 跳石头
- P1902 刺杀大使
- P1314 聪明的质监员
- P1083 借教室
- P4343 [SHOI2015]自动刷题机
一元三次方程求解
# [NOIP2001 提高组] 一元三次方程求解
## 题目描述
有形如:$a x^3 + b x^2 + c x + d = 0$ 这样的一个一元三次方程。给出该方程中各项的系数($a,b,c,d$ 均为实数),并约定该方程存在三个不同实根(根的范围在 $-100$ 至 $100$ 之间),且根与根之差的绝对值 $\ge 1$。要求由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后 $2$ 位。
提示:记方程 $f(x) = 0$,若存在 $2$ 个数 $x_1$ 和 $x_2$,且 $x_1 < x_2$,$f(x_1) \times f(x_2) < 0$,则在 $(x_1, x_2)$ 之间一定有一个根。
## 输入格式
一行,$4$ 个实数 $a, b, c, d$。
## 输出格式
一行,$3$ 个实根,从小到大输出,并精确到小数点后 $2$ 位。
## 样例 #1
### 样例输入 #1
```
1 -5 -4 20
```
### 样例输出 #1
```
-2.00 2.00 5.00
```
## 提示
**【题目来源】**
NOIP 2001 提高组第一题package _02_基础算法._03_二分答案._01_P1024_一元三次方程求解_尝试2;
import java.io.BufferedInputStream;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
a = sc.nextDouble();
b = sc.nextDouble();
c = sc.nextDouble();
d = sc.nextDouble();
List<Double> ans = new ArrayList<>();
for (double x = -100; x <= 100; x+=0.001) {
if(Math.abs(fun(x))<0.01) {
ans.add(x);
x+=1;
}
if(ans.size()>=3) {
break;
}
}
for (Double val : ans) {
System.out.printf("%.2f ",val);
}
}
static double a, b, c, d;
static double fun(double x) {
return a * x * x * x + b * x * x + c * x + d;
}
}