
蓝桥杯培训内部2014年预赛讲解学习笔记
蓝桥杯培训内部2014年预赛讲解学习笔记
目录
李白打酒

public class _01_李白打酒 {
public static void main(String[] args) {
dfs(2, 5, 10);
System.out.println(count);
/*
* 输出:
* ababbbbbabababb
* abbabbabbbababb
* abbabbbaabbbabb
* abbabbbabaabbbb
* abbbaabbabbbabb
* abbbaabbbaabbbb
* abbbabaabbabbbb
* baababbbbbababb
* baabbabbabbbabb
* baabbabbbaabbbb
* baabbbaabbabbbb
* babaababbbbbabb
* babaabbabbabbbb
* bababaababbbbbb
* 14
*/
}
static int count = 0;
static StringBuilder sb = new StringBuilder();
static void dfs(int restWine/* 剩多少酒 */, int restShop/* 剩多少店没逢 */, int restFllower/* 剩多少朵花没遇 */) {
if (restWine == 0 && restFllower == 0 && restShop == 0/* 喝完酒,遇完花,逢完店 */) {
String string = sb.toString();
if (string.charAt(string.length() - 1) == 'b'/* 只统计最后遇到的是花的情况 */) {
System.out.println(string);
count++;// 找到一种情况
}
} else {
if (0 < restShop /* 还能遇到店 */ && restWine != 0 /* 是否需要保证没有提前把酒喝完? 实测对最终统计结果没有影响,因为统计的是遇到花后喝掉一斗后剩余酒为0的情况,这就要求剩余酒量在遇到最后一朵花前至少为1 */) {
sb.append("a");
dfs(restWine + restWine/* 加一倍 */, restShop - 1, restFllower);
sb.deleteCharAt(sb.length() - 1);// 回溯
}
if ( 0 < restFllower /* 还能遇到花 */ && restWine != 0 /* 是否需要保证还有酒?,如果没有酒还喝酒就会导致剩余酒为负数,这种情况最后不会被统计在内,所以这个条件可写可不写,写就是剪枝的作用 */) {
sb.append("b");
dfs(restWine - 1/* 喝一斗 */, restShop, restFllower - 1);
sb.deleteCharAt(sb.length() - 1);// 回溯
}
}
}
}大数阶乘


数组长度的粗略估计
也可以这样想,把 5000!看做是 5000 个 四位数相乘,
一个四位数最多是9999,所以再简单粗暴点,直接看做是10000,
这样也是就5000 个 10000相乘,结果就是5的后面 4x5000个0,也就是有 20000位
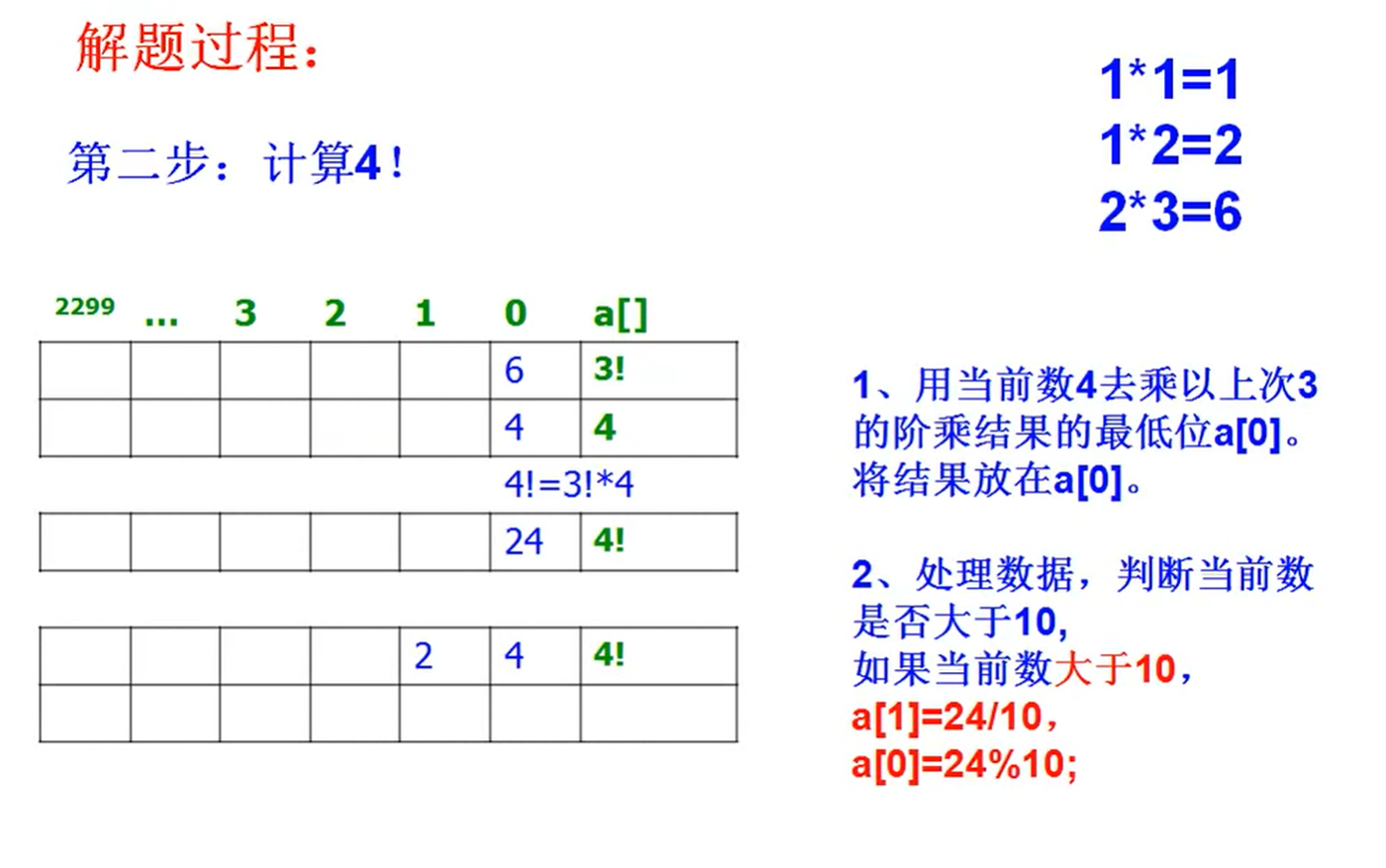
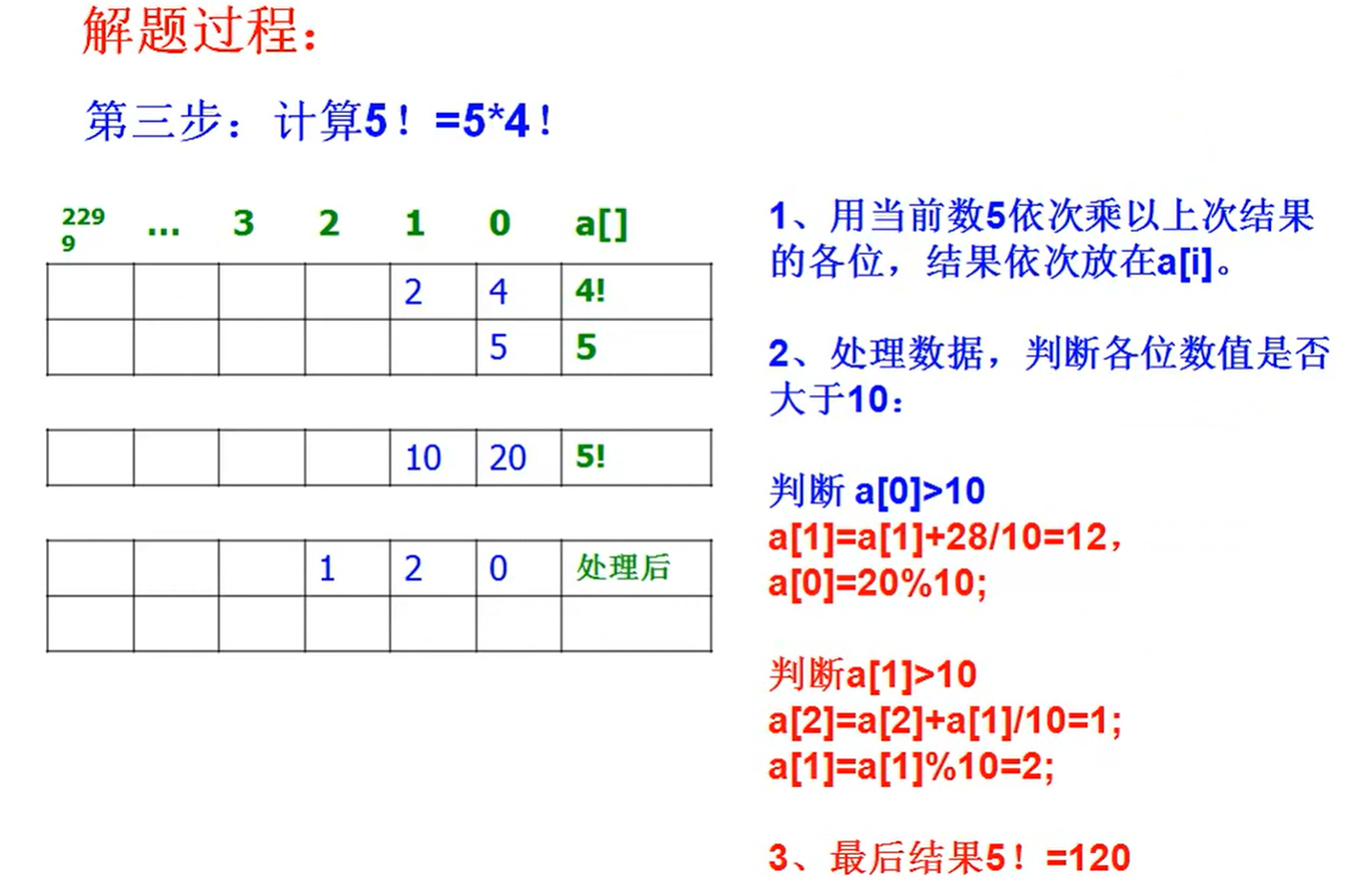
计算过程
假设已经计算出3的阶乘的每一位的数值的数组了,现在要计算4的阶乘,
只需要把4乘上上一轮的数组中的每一位数,
然后在统一处理进位的问题
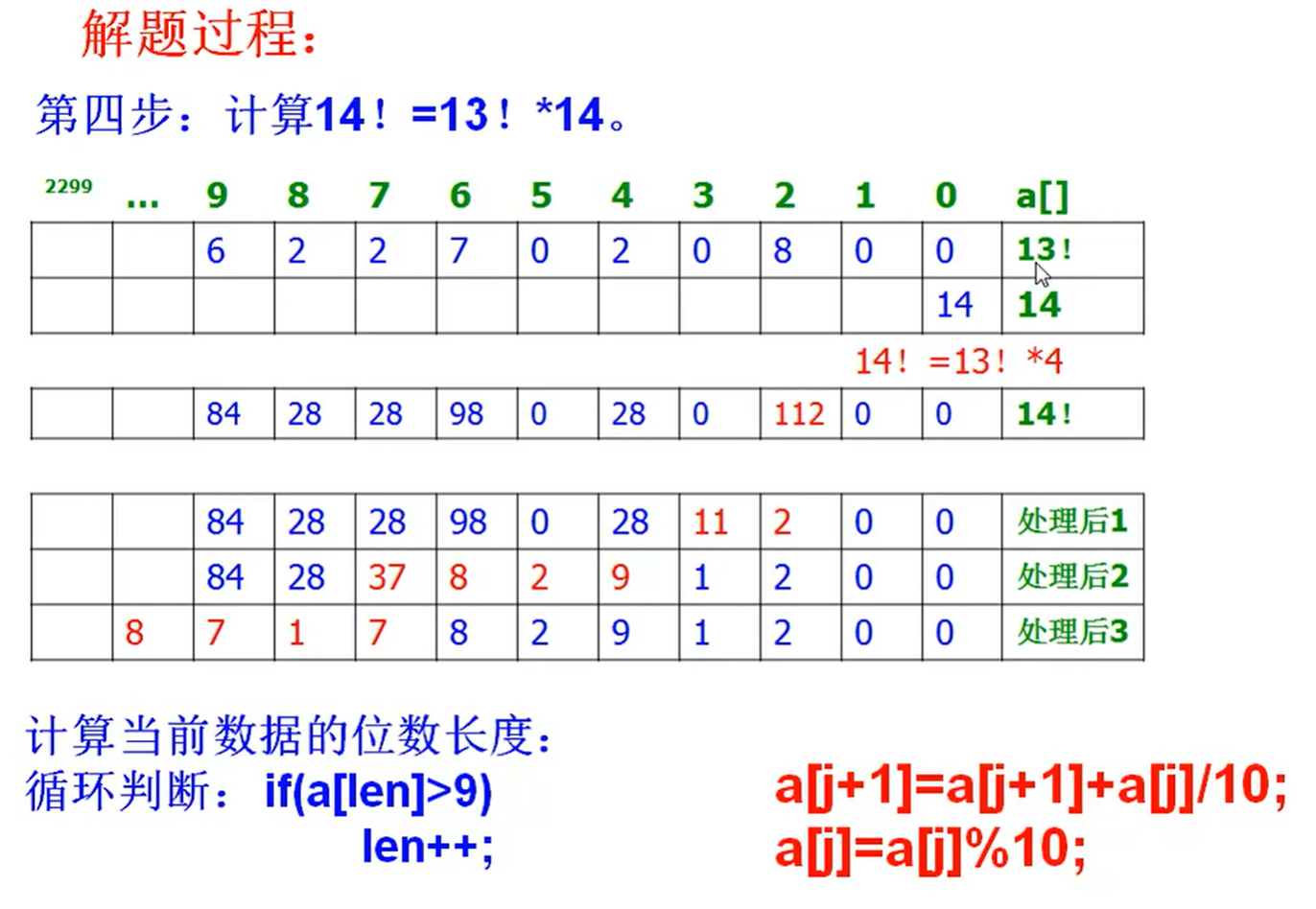
数据长度的更新
可以在本轮的最后一位上判断是否存在进位,存在就扩展位数
完整实现
import java.util.Arrays;
public class _02_大数阶乘 {
public static void main(String[] args) {
// 输出为:3628800 和计算器计算结果一致
System.out.println(comput(10));
// 输出为:93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
System.out.println(comput(100));
}
/*
* num[j]中存的数的最大值是9,
* num[j] 中能存储的最大值是Integer.MAX_VALUE
* 所以N的最大值至少是 Integer.MAX_VALUE/9
*/
static String comput(int N) {
int[] num = new int[N * String.valueOf(N).length()/* 注意这个数组的大小是如何计算的,直接假设是n个和n位数相同的数相乘 */];
num[0] = 1; // 初始化为1的阶乘
int len = 1;// 数组中的有效位数为1
// 依次求2的阶乘,3的阶乘,4的阶乘....指导n的阶乘
for (int i = 2; i <= N; i++) {
for (int j = 0; j < len; j++) {
num[j] *= i;
}
// System.out.println(Arrays.toString(num));
for (int j = 0; j < len; j++) {
if (j == len - 1 /* 已在最后一位(最高位) */ && num[len - 1] / 10 != 0/* 还有进位未处理 */) {
len++;
}
num[j + 1] += num[j] / 10;// 处理进位,低位向高位进
num[j] %= 10;// 处理当前位,对10取余
}
// System.out.println(Arrays.toString(num));
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < len; i++) {
sb.append(num[i]);
}
sb.reverse();// 反转
return sb.toString();
}
}单词拼接


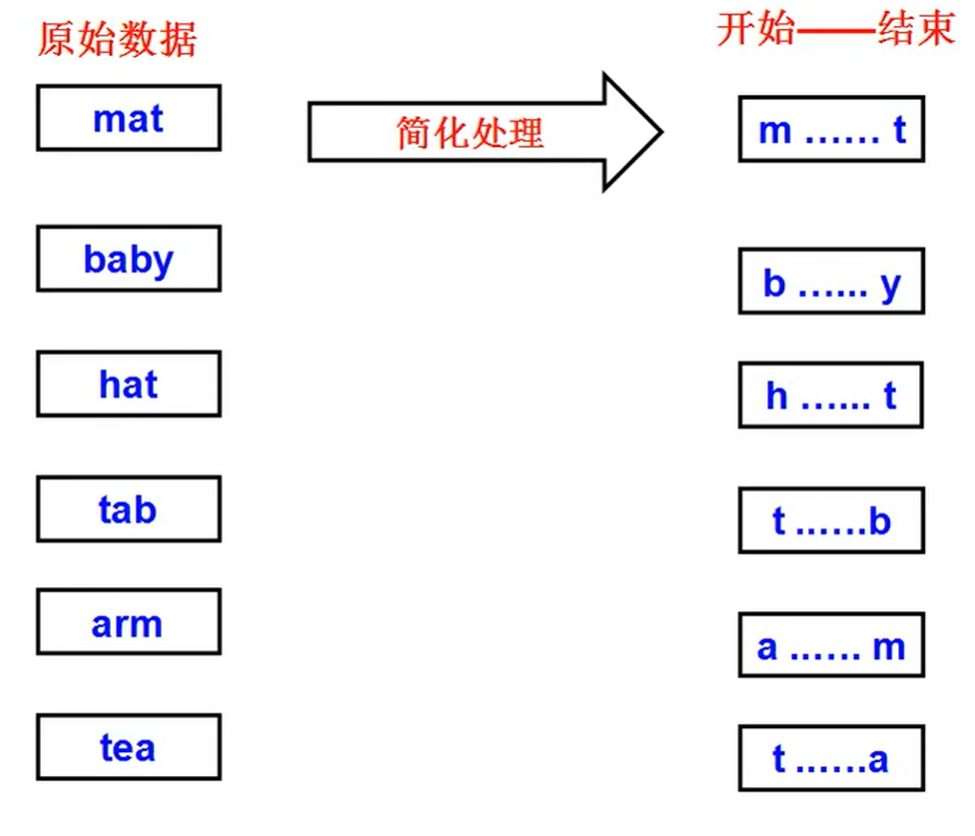
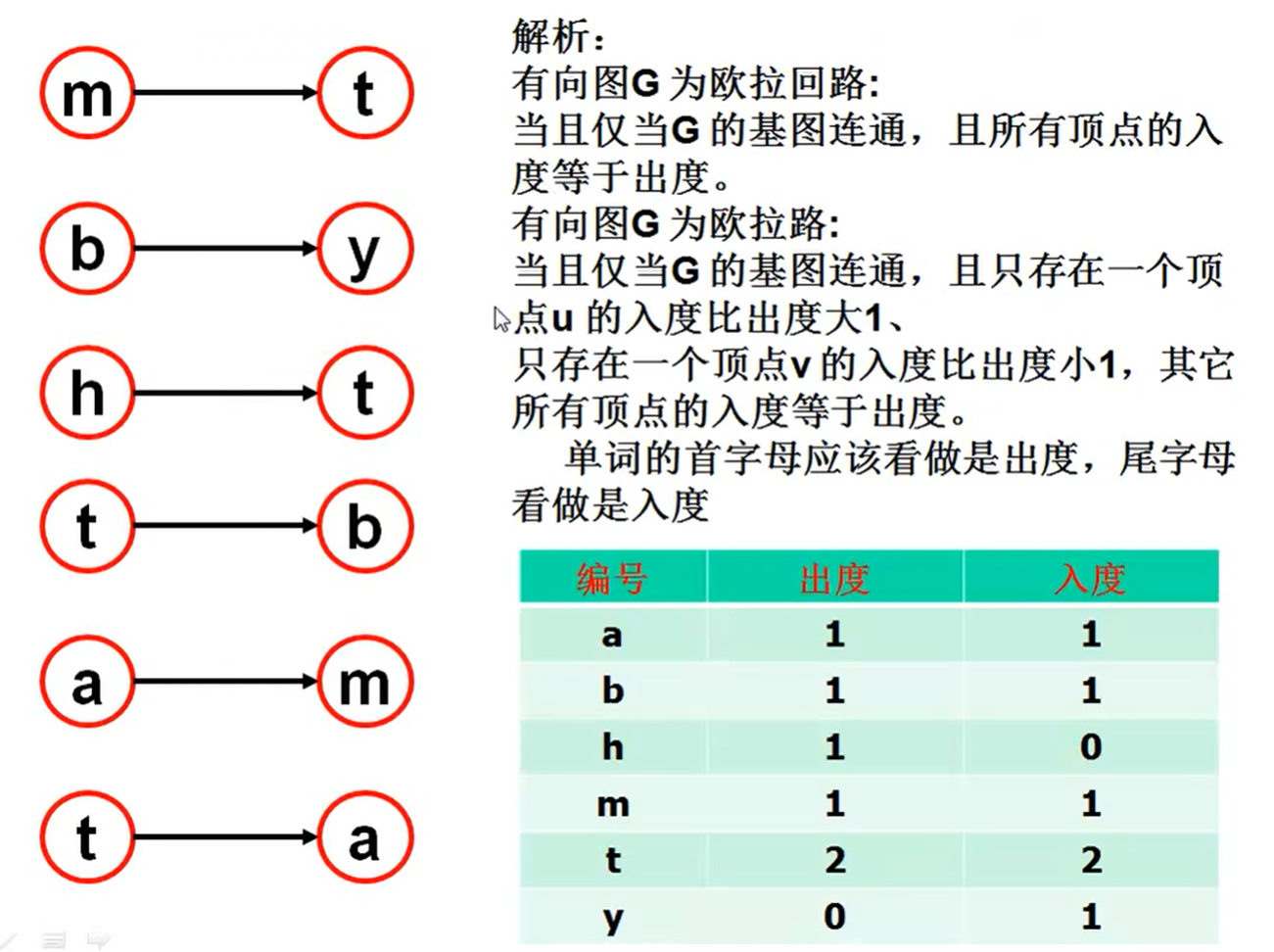
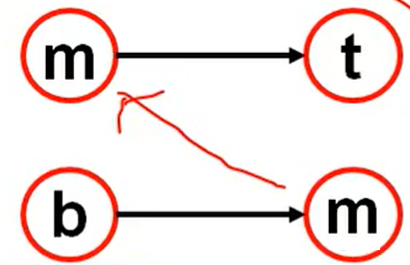
欧拉路
- 整个图连通【重要前提】
- 只有一个节点的入度比出度大1
- 只有一个节点的出度比入度小1
- 换句话说,有一节点入度为0出度为1,有另一节点出度为0,入度为1
- 入度为0的点就是路径入口,出度为0的点就是路径出口
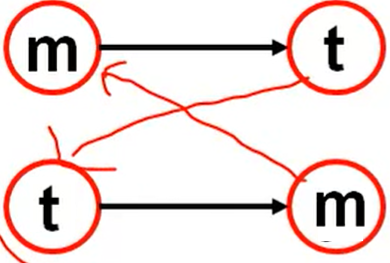
欧拉回路
- 整个图连通【重要前提】
- 所有顶点的入度等于出度
- 就是说可以从任何一个节点作为节点,然后走完整个图的所有节点
- 这样起点可以是任何位置。
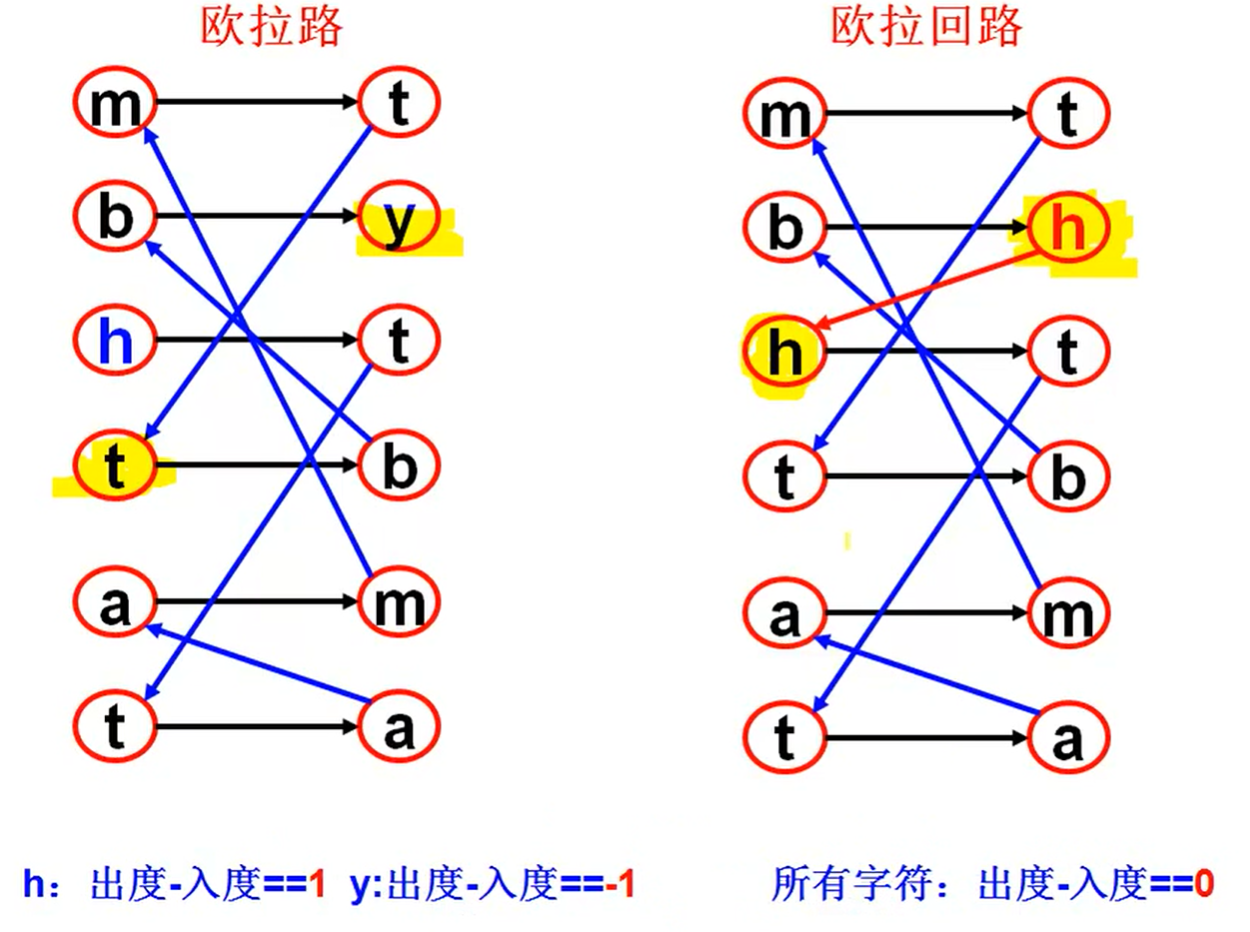


中途学习eclipse使用的笔记

我的暴力解法:字典序预先排序+DFS+HashMap+回溯
输入
2
6
mat
baby
hat
tab
arm
tea
3
oak
maple
elm
输出
hat.tea.arm.mat.tab.baby
***import java.util.*;
public class _03_单词拼接 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = Integer.valueOf(sc.nextLine());
List<String> res = new LinkedList<>();
for (int i = 0; i < N; i++) {
Graph g = new Graph();
g.buildGraph(sc);
res.add(g.dfs(null));// 把结果先存到数组中
}
sc.close();
for (String str : res) {
if (str != null) {
System.out.println(str);
} else {
System.out.println("***");
}
}
}
}
class Node implements Comparable<Node> {
Character start, ended;
String content;
public Node(String content) {
super();
this.content = content;
this.start = content.charAt(0);
this.ended = content.charAt(content.length() - 1);
}
@Override
public int compareTo(Node o) {
// 这样先排序,再 DFS 搜索,找到的第一个答案就是题目要的字典序最小的答案
// 否则则需要 DFS 搜索出所有的结果,然后再比较字典序
// 这句是最关键的,有题目问,把一个字符串数组中的字符串拼接起来,找到使其拼接结果的字典序最小的字符串。其方法就是先对数组中的字符串排序,排序的比较方法就是这个函数:
return (this.content + o.content).compareTo(o.content + this.content);
}
}
class Edge {// 写了但没用
Node from, to;
public Edge(Node from, Node to) {
super();
this.from = from;
this.to = to;
}
}
class Graph {
List<Node> nodes = new LinkedList<>();
List<Edge> edges = new LinkedList<>();// 没有用
Set<Node> used = new HashSet<>();
HashMap<Character, List<Node>> startMap = new HashMap<>();// 这个实际上没有用
HashMap<Character, List<Node>> endedMap = new HashMap<>();// 只有这个有用
void buildGraph(Scanner sc) {
int M = Integer.valueOf(sc.nextLine());// 注意要统一使用nextLine()
for (int i = 0; i < M; i++) {
String word = sc.nextLine();
Node node = new Node(word);
nodes.add(node);
if (!startMap.containsKey(node.start)/* 防止未初始化 */) {
startMap.put(node.start, new LinkedList<>());
}
if (!endedMap.containsKey(node.ended)) {
endedMap.put(node.ended, new LinkedList<>());
}
startMap.get(node.start).add(node);
endedMap.get(node.ended).add(node);
}
Collections.sort(nodes);// 排序,保证字典序最小
for(List<Node> list :startMap.values()) {
Collections.sort(list);// 排序,保证字典序最小
}
for(List<Node> list :endedMap.values()) {
Collections.sort(list);// 排序,保证字典序最小
}
}
LinkedList<String> result = new LinkedList<>();
String dfs(Node current) {
if (used.size() == nodes.size()) {
StringBuilder sb = new StringBuilder();
for (String item : result) {
sb.append(item);
sb.append('.');
}
if (result.size() >= 1) {
sb.deleteCharAt(sb.length() - 1);
}
return sb.toString();
} else if (current == null) {
// 确定开头的元素
for (Node cur : nodes /* 把所有节点依次当做开头位置,依次尝试 */) {
used.add(cur);// 标记为使用
result.add(cur.content);
String res = dfs(cur);
result.removeLast();// 回溯
used.remove(cur);// 回溯
if (res != null) {
return res;// 找到答案,因为节点已经按字典序排序了,拼接起来的字符串一定是字典序最小的
}
}
} else {
// 确定当前字符串的下一个字符串
if (startMap.containsKey(current.ended)/*直接查表:看是否有一个单词的开头是当前单词的结尾*/) {
for (Node next : startMap.get(current.ended) /* 当前字符串的结尾,是下一个字符串的开头 */) {
if (!used.contains(next)/* never used */) {
used.add(next);// 标记为使用
result.add(next.content);
String res = dfs(next);
result.removeLast();// 回溯
used.remove(next);// 回溯
if (res != null) {
return res;// 找到答案
}
}
}
}
}
return null;// 没找到
}
}ACM导弹拦截
防御导弹
Problem
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够达到任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在使用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
Input
最多20个整数,分别表示导弹依次飞来的高度(雷达给出高度数据是不大于30000的正整数)
Output
两个整数M和N。表示:这套系统最多能拦截 M 枚导弹,如果要拦截所有导弹最少要配备 N 套这种导弹系统。
Sample Input
300 250 275 252 200 138 245
Sample Output
5 2解题尝试1
实际上这个思路对N的求解似乎是正确的。
对M的求解似乎是错误的
这里对题意错误了,以为是导弹依次来袭,然后依次得知高度信息,实际上这里的意思是导弹同时来袭,同时得到高度信息。
是在知道所有导弹的高度信息的情况下做决策,而不是在依次知道高度信息的情况下做决策。
思路
最多20个整数就是最多20发导弹,
先考虑两个极端情况
假设来袭导弹的高度是递增的,那么拦截第一发后导弹后,第二发导弹就必须要另一套系统来拦截。
这样每一发导弹都需要另一套系统来拦截
假设来袭导弹的高度是递减的,那么一套系统就可以拦截所有导弹。
可以这样想,用现实的眼光来看,假设有20套系统,现在有一发导弹来袭,让哪一套系统来拦截?
当然是让拦截代价最低的系统来拦截,而拦截代价就是:(开火前能打高度 减去 开火后能打高度),
这样对所有系统的剩余拦截高度范围的消耗最小。
输入
300 250 275 252 200 138 245
[138, 245, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001, 30001]
输出:
[4, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4
2import java.util.*;
public class _04_ACM导弹拦截 {
public static void main(String[] args) {
// 最多20发导弹
Scanner sc = new Scanner(System.in);
String[] inputs = sc.nextLine().split(" ");
int[] heights = new int[inputs.length];// 20发导弹高度信息
for (int i = 0; i < heights.length; i++) {
heights[i]= Integer.valueOf(inputs[i]);
}
// 对于只有一套系统的情况,
int sysOne = 30001;//剩余可拦截高度信息
int cntOne = 0;//单系统拦截的导弹数统计
for (int i = 0; i < heights.length; i++) {
int targetHeight = heights[i];// 目标高度
if(sysOne > targetHeight) {
sysOne = targetHeight;
cntOne++;
}
}
// 对于有20套系统的情况:
int len = 1;// 启用的拦截系统数
int[] sys = new int[20];// 20套导弹拦截系统 剩余可拦截高度信息
int[] cnt = new int[20];// 20套导弹拦截系统 单系统拦截的导弹数
for (int i = 0; i < sys.length; i++) {
sys[i]=30001;// 导弹的高度不超过30000(可能会等于),则系统初始最高可打的高度也设置成这个
}
for (int i = 0; i < heights.length; i++) {// 依次处理来袭导弹的高度信息
int targetHeight = heights[i];// 目标高度
int minCost = Integer.MAX_VALUE;
int bestSys = -1;// 最终决定让谁开火
for (int j = 0; j < len; j++) {// 遍历20套系统
int cost = sys[j] - targetHeight;// 找到代价最小的策略
if(sys[j] > targetHeight/*可以击落*/ && cost<minCost/*代价最小*/) {
minCost=cost;
bestSys = j;
}
}
// 实在是无法拦截才启动增添新系统
if(bestSys==-1/*依然无法*/&&len<sys.length/*还能增加系统,实际上不需要这个判断*/) {
++len;
bestSys = len-1;
}
// 拦截
sys[bestSys] = targetHeight;
cnt[bestSys]++;// 统计开火次数
}
System.out.println(Arrays.toString(sys));
System.out.println(Arrays.toString(cnt));
System.out.println(cntOne);
System.out.println(len);
}
}解题尝试2:对于M的求解,似乎就是求最长递减子序列
思路
实际上要明白一个问题,是不是每一发导弹都是能拦截就拦截,
如果是能拦截就拦截,那如果第一发导弹的高度是1,后续导弹的高度是 5 4 3 2
则只能拦截到第一发导弹,后续4发导弹都无法拦截,整个拦截系统都因第一发导弹而瘫痪
如果不拦截第一发导弹,则后续四发导弹都能拦截,这应该才是最优解。
对于任何一发导弹是否拦截,都要看后续有没有高度连续递减的导弹可以拦截。
对于M的求解,似乎就是求最长递减子序列。
输入
300 250 275 252 200 138 245
程序输出(不应该输出4)
4 2import java.util.*;
public class _05_ACM导弹拦截_错误解法求最长递减子序列 {
public static void main(String[] args) {
// 最多20发导弹
Scanner sc = new Scanner(System.in);
String[] inputs = sc.nextLine().split(" ");
int[] heights = new int[inputs.length];// 20发导弹高度信息
for (int i = 0; i < heights.length; i++) {
heights[i] = Integer.valueOf(inputs[i]);
}
// 求最长递减子序列
// 对于只有一套系统的情况,
int maxLen = Integer.MIN_VALUE;
for(int startIdx = 0/*开始位置*/;startIdx<heights.length;startIdx++) {
int len =1;
int prev= heights[startIdx];
for(int curIdx=startIdx+1;curIdx<heights.length;curIdx++) {
if(prev>heights[curIdx]) {
len++;
prev=heights[curIdx];// 这一步就错了,下一步是递减的,但下一步并不一定是长的走法,也许跳过这一步能走得更远
}
}
System.out.println(len);
if(maxLen<len) {
maxLen=len;
}
}
// 对于有20套系统的情况:
int len = 1;// 启用的拦截系统数
int[] sys = new int[20];// 20套导弹拦截系统 剩余可拦截高度信息
int[] cnt = new int[20];// 20套导弹拦截系统 单系统拦截的导弹数
for (int i = 0; i < sys.length; i++) {
sys[i] = 30001;// 导弹的高度不超过30000(可能会等于),则系统初始最高可打的高度也设置成这个
}
for (int i = 0; i < heights.length; i++) {// 依次处理来袭导弹的高度信息
int targetHeight = heights[i];// 目标高度
int minCost = Integer.MAX_VALUE;
int bestSys = -1;// 最终决定让谁开火
for (int j = 0; j < len; j++) {// 遍历20套系统
int cost = sys[j] - targetHeight;// 找到代价最小的策略
if (sys[j] > targetHeight/* 可以击落 */ && cost < minCost/* 代价最小 */) {
minCost = cost;
bestSys = j;
}
}
// 实在是无法拦截才启动增添新系统
if (bestSys == -1/* 依然无法 */ && len < sys.length/* 还能增加系统,实际上不需要这个判断 */) {
++len;
bestSys = len - 1;
}
// 拦截
sys[bestSys] = targetHeight;
cnt[bestSys]++;// 统计开火次数
}
System.out.println(maxLen+" "+len);
}
}解题尝试3:正确解法,动态规划求解M,求最长递减子序列
动态规划求最长递减子序列
看这样一个例子:
300 250 275 252 200 138 245
考虑以第1个数 300 结尾的递减子序列的长度:为1 就是 [300] 为什么? 因为往前看没有任何数比自身大,那么算算上自身这一位 就是 1
考虑以第2个数 250 结尾的递减子序列的长度:为2 就是 [300,250] 为什么? 因为往前看会有最近的300比自身大,而以300结尾的最长递减子序列长度为1,那么算算上自身这一位 就是 2
考虑以第3个数 275 结尾的递减子序列的长度:为2 就是 [300,275] 为什么? 因为往前看会有最近的300比自身大,而以300结尾的最长递减子序列长度为1,那么算算上自身这一位 就是 2
考虑以第4个数 252 结尾的递减子序列的长度:为3 就是 [300,275,252] 为什么? 因为往前看会有最近的275比自身大,而以275结尾的最长递减子序列长度为2,那么算算上自身这一位 就是 3
考虑以第5个数 200 结尾的递减子序列的长度:为4 就是 [300,275,252,200] 为什么? 因为往前看会有最近的252比自身大,而以252结尾的最长递减子序列长度为3,那么算算上自身这一位 就是 4
考虑以第6个数 138 结尾的递减子序列的长度:为5 就是 [300,275,252,200,138] 为什么? 因为往前看会有最近的200比自身大,而以200结尾的最长递减子序列长度为4,那么算算上自身这一位 就是 5
考虑以第7个数 245 结尾的递减子序列的长度:为4 就是 [300,275,252,245] 为什么? 因为往前看会有最近的252比自身大,而以252结尾的最长递减子序列长度为3,那么算算上自身这一位 就是 4输入
300 250 275 252 200 138 245
程序输出(输出正确!!!!)
5 2import java.util.*;
public class _06_ACM导弹拦截_动态规划求最长递减子序列 {
public static void main(String[] args) {
// 最多20发导弹
Scanner sc = new Scanner(System.in);
String[] inputs = sc.nextLine().split(" ");
int[] heights = new int[inputs.length];// 20发导弹高度信息
for (int i = 0; i < heights.length; i++) {
heights[i] = Integer.valueOf(inputs[i]);
}
// 求最长递减子序列
// 对于只有一套系统的情况,
int[] dp=new int[heights.length];
int maxLen = Integer.MIN_VALUE;
for(int curIdx = 0/*开始位置*/;curIdx<heights.length;curIdx++) {
int len = 1 ;
for(int preIdx=curIdx;0<=preIdx;preIdx--) {// 往前找
if(heights[preIdx]>heights[curIdx]) {
len+=dp[preIdx];
break;
}
}
dp[curIdx]=len;
if(maxLen<len) {
maxLen=len;
}
}
System.out.println(Arrays.toString(dp));
// 对于有20套系统的情况:
int len = 1;// 启用的拦截系统数
int[] sys = new int[20];// 20套导弹拦截系统 剩余可拦截高度信息
int[] cnt = new int[20];// 20套导弹拦截系统 单系统拦截的导弹数
for (int i = 0; i < sys.length; i++) {
sys[i] = 30001;// 导弹的高度不超过30000(可能会等于),则系统初始最高可打的高度也设置成这个
}
for (int i = 0; i < heights.length; i++) {// 依次处理来袭导弹的高度信息
int targetHeight = heights[i];// 目标高度
int minCost = Integer.MAX_VALUE;
int bestSys = -1;// 最终决定让谁开火
for (int j = 0; j < len; j++) {// 遍历20套系统
int cost = sys[j] - targetHeight;// 找到代价最小的策略
if (sys[j] > targetHeight/* 可以击落 */ && cost < minCost/* 代价最小 */) {
minCost = cost;
bestSys = j;
}
}
// 实在是无法拦截才启动增添新系统
if (bestSys == -1/* 依然无法 */ && len < sys.length/* 还能增加系统,实际上不需要这个判断 */) {
++len;
bestSys = len - 1;
}
// 拦截
sys[bestSys] = targetHeight;
cnt[bestSys]++;// 统计开火次数
}
System.out.println(maxLen+" "+len);
}
}括号配对问题

非常简单
单栈实现(我认为是最优解)
输入
5
{}{}
[][]
()()
[()]{}
[[[}}}
输出
Yes
Yes
Yes
Yes
Noimport java.util.*;
public class _08_括号配对问题_单栈实现_最优解 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = Integer.valueOf(sc.nextLine());
List<Boolean> result = new LinkedList<>();
for (int i = 0; i < N; i++) {
result.add(check(sc.nextLine()));
}
sc.close();
for (Boolean res : result) {
if (res)
System.out.println("Yes");
else
System.out.println("No");
}
}
static boolean check(String expression) {
Stack<Character> left = new Stack<>();
for (char ch : expression.toCharArray()) {
if (ch == '(' || ch == '[' || ch == '{'/*右括号*/) {
left.push(ch);// 压入栈
continue;
}else if(ch == ')' || ch == ']' || ch == '}'/*左括号*/) {
Character R = ch;
Character L= !left.isEmpty() ? left.pop():null;
if(L!=null && ((L == '[' && R == ']') || (L == '(' && R == ')') || (L == '{' && R == '}'))/*右括号应当能和栈顶元素匹配*/) {
continue;
}else {
return false;
}
}
}
return left.size()==0;// 一定要栈空!
}
}双栈实现:弄复杂了
import java.util.*;
public class _08_括号配对问题_单栈实现_最优解 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = Integer.valueOf(sc.nextLine());
List<Boolean> result = new LinkedList<>();
for (int i = 0; i < N; i++) {
result.add(check(sc.nextLine()));
}
sc.close();
for (Boolean res : result) {
if (res)
System.out.println("Yes");
else
System.out.println("No");
}
}
static boolean check(String expression) {
Stack<Character> left = new Stack<>();
for (char ch : expression.toCharArray()) {
if (ch == '(' || ch == '[' || ch == '{'/*右括号*/) {
left.push(ch);// 压入栈
continue;
}else if(ch == ')' || ch == ']' || ch == '}'/*左括号*/) {
Character R = ch;
Character L= !left.isEmpty() ? left.pop():null;
if(L!=null && ((L == '[' && R == ']') || (L == '(' && R == ')') || (L == '{' && R == '}'))/*右括号应当能和栈顶元素匹配*/) {
continue;
}else {
return false;
}
}
}
return true;
}
}吝啬的国度


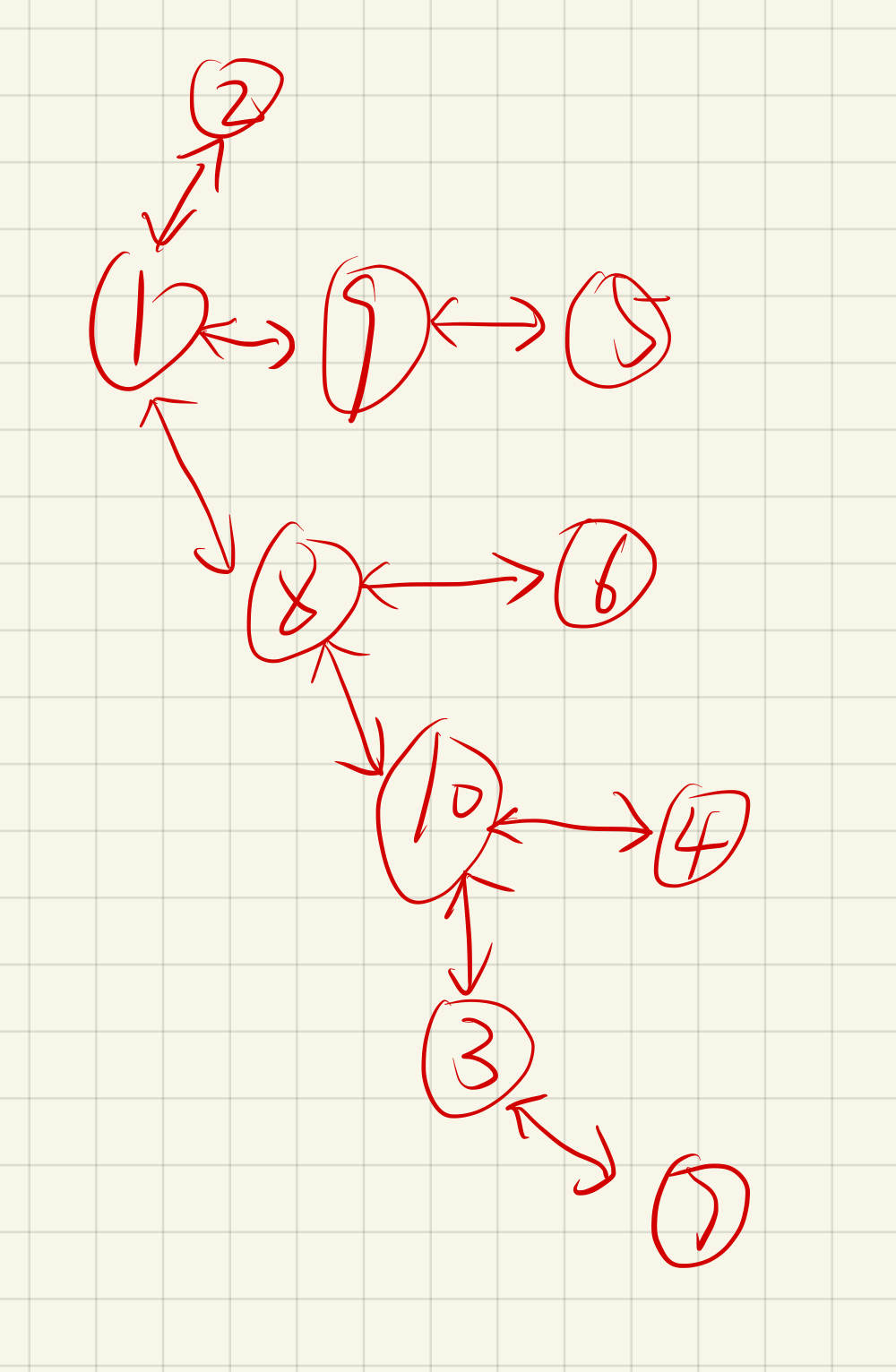
样例输入:
1
10 1
1 9
1 8
8 10
10 3
8 6
1 2
10 4
9 5
3 7
样例输出:
-1 1 10 10 9 8 3 1 1 8广度优先遍历_非递归实现
程序输入输出
输入
1
10 1
1 9
1 8
8 10
10 3
8 6
1 2
10 4
9 5
3 7
输出
[-1, 1, 10, 10, 9, 8, 3, 1, 1, 8]
输入
1
10 8
1 9
1 8
8 10
10 3
8 6
1 2
10 4
9 5
3 7
输出
[8, 1, 10, 10, 9, 8, 3, -1, 1, 8]import java.util.*;
public class _09_吝啬的国度_广度优先遍历bfs_非递归实现 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Graph g = new Graph();
int k = sc.nextInt();
for (int i = 0; i < k; i++) {
g.create(sc);
System.out.println(Arrays.toString(g.bfs()));
}
}
static class Node {
Set<Edge> froms = new HashSet<>();
Set<Edge> nexts = new HashSet<>();
int idx;
public Node(int idx) {
super();
this.idx = idx;
}
}
static class Edge {
Node from, to;
public Edge(Node from, Node to) {
super();
this.from = from;
this.to = to;
}
}
static class Graph {
Set<Node> nodes = new HashSet<>();
Set<Edge> edges = new HashSet<>();
Map<Integer, Node> idxToNode = new HashMap<>();
int initIdx;
int N;
void create(Scanner sc) {
N = sc.nextInt();// 总节点数
initIdx = sc.nextInt();// 初始位置
for (int i = 0; i < N - 1/* n-1条边 */; i++) {
int idxA = sc.nextInt();
int idxB = sc.nextInt();
// System.out.println(idxA + "<--->" + idxB);
Node nodeA, nodeB;
if (!idxToNode.containsKey(idxA)) {
nodeA = new Node(idxA);
idxToNode.put(idxA, nodeA);
nodes.add(nodeA);
}
if (!idxToNode.containsKey(idxB)) {
nodeB = new Node(idxB);
idxToNode.put(idxB, nodeB);
nodes.add(nodeB);
}
nodeA = idxToNode.get(idxA);
nodeB = idxToNode.get(idxB);
Edge edgeA2B = new Edge(nodeA, nodeB);// 无向图
Edge edgeB2A = new Edge(nodeB, nodeA);
// nodeA.froms.add(edgeB2A);
// nodeB.froms.add(edgeA2B);
nodeA.nexts.add(edgeA2B);
nodeB.nexts.add(edgeB2A);
edges.add(edgeA2B);
edges.add(edgeB2A);
}
}
// Map<Integer, Integer> result = new HashMap<>();
int[] bfs() {
int[] result= new int[N];
Set<Node> visited = new HashSet<>();
Queue<Node> queue = new LinkedList<>();
Node from = idxToNode.get(initIdx);
visited.add(from);
result[from.idx - 1] = -1;
queue.add(from);
while (!queue.isEmpty()) {
Node cur = queue.poll();
visited.add(cur);
for (Edge edge : cur.nexts) {
Node next = edge.to;
if (!visited.contains(next)) {
result[next.idx - 1] = cur.idx;
queue.add(next);
}
}
}
return result;
}
}
}深度优先遍历实现_非递归实现
程序输入输出
输入
1
10 1
1 9
1 8
8 10
10 3
8 6
1 2
10 4
9 5
3 7
输出
[-1, 1, 10, 10, 9, 8, 3, 1, 1, 8]import java.util.*;
public class _09_吝啬的国度_深度度优先dfs_非递归实现 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Graph g = new Graph();
int k = sc.nextInt();
for (int i = 0; i < k; i++) {
g.create(sc);
System.out.println(Arrays.toString(g.dfs()));
}
}
static class Node {
Set<Edge> froms = new HashSet<>();
Set<Edge> nexts = new HashSet<>();
int idx;
public Node(int idx) {
super();
this.idx = idx;
}
}
static class Edge {
Node from, to;
public Edge(Node from, Node to) {
super();
this.from = from;
this.to = to;
}
}
static class Graph {
Set<Node> nodes = new HashSet<>();
Set<Edge> edges = new HashSet<>();
Map<Integer, Node> idxToNode = new HashMap<>();
int initIdx;
int N;
void create(Scanner sc) {
N = sc.nextInt();// 总节点数
initIdx = sc.nextInt();// 初始位置
for (int i = 0; i < N - 1/* n-1条边 */; i++) {
int idxA = sc.nextInt();
int idxB = sc.nextInt();
// System.out.println(idxA + "<--->" + idxB);
Node nodeA, nodeB;
if (!idxToNode.containsKey(idxA)) {
nodeA = new Node(idxA);
idxToNode.put(idxA, nodeA);
nodes.add(nodeA);
}
if (!idxToNode.containsKey(idxB)) {
nodeB = new Node(idxB);
idxToNode.put(idxB, nodeB);
nodes.add(nodeB);
}
nodeA = idxToNode.get(idxA);
nodeB = idxToNode.get(idxB);
Edge edgeA2B = new Edge(nodeA, nodeB);// 无向图
Edge edgeB2A = new Edge(nodeB, nodeA);
// nodeA.froms.add(edgeB2A);
// nodeB.froms.add(edgeA2B);
nodeA.nexts.add(edgeA2B);
nodeB.nexts.add(edgeB2A);
edges.add(edgeA2B);
edges.add(edgeB2A);
}
}
// Map<Integer, Integer> result = new HashMap<>();
// 深度优先遍历
int[] dfs() {
Set<Node> visited = new HashSet<>();
int[] result= new int[N];
Node from = idxToNode.get(initIdx);
Stack<Node> stack = new Stack<>();
visited.add(from);
result[from.idx - 1] = -1;
stack.push(from);
while (!stack.isEmpty()) {
Node cur = stack.pop();
visited.add(cur);
for (Edge edge : cur.nexts) {
Node next = edge.to;
if (!visited.contains(next)) {
result[next.idx - 1] = cur.idx;
stack.push(next);
}
}
}
return result;
}
}
}深度优先_递归实现
import java.util.*;
public class _09_吝啬的国度_深度优先遍历dfs_递归实现 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Graph g = new Graph();
int k = sc.nextInt();
for (int i = 0; i < k; i++) {
g.create(sc);
g.dfs(null);
System.out.println(Arrays.toString(g.result));
}
}
static class Node {
Set<Edge> froms = new HashSet<>();
Set<Edge> nexts = new HashSet<>();
int idx;
public Node(int idx) {
super();
this.idx = idx;
}
}
static class Edge {
Node from, to;
public Edge(Node from, Node to) {
super();
this.from = from;
this.to = to;
}
}
static class Graph {
Set<Node> nodes = new HashSet<>();
Set<Edge> edges = new HashSet<>();
Map<Integer, Node> idxToNode = new HashMap<>();
int initIdx;
int N;
void create(Scanner sc) {
N = sc.nextInt();// 总节点数
result = new int[N];
initIdx = sc.nextInt();// 初始位置
for (int i = 0; i < N - 1/* n-1条边 */; i++) {
int idxA = sc.nextInt();
int idxB = sc.nextInt();
// System.out.println(idxA + "<--->" + idxB);
Node nodeA, nodeB;
if (!idxToNode.containsKey(idxA)) {
nodeA = new Node(idxA);
idxToNode.put(idxA, nodeA);
nodes.add(nodeA);
}
if (!idxToNode.containsKey(idxB)) {
nodeB = new Node(idxB);
idxToNode.put(idxB, nodeB);
nodes.add(nodeB);
}
nodeA = idxToNode.get(idxA);
nodeB = idxToNode.get(idxB);
Edge edgeA2B = new Edge(nodeA, nodeB);// 无向图
Edge edgeB2A = new Edge(nodeB, nodeA);
// nodeA.froms.add(edgeB2A);
// nodeB.froms.add(edgeA2B);
nodeA.nexts.add(edgeA2B);
nodeB.nexts.add(edgeB2A);
edges.add(edgeA2B);
edges.add(edgeB2A);
}
}
// Map<Integer, Integer> result = new HashMap<>();
Set<Node> visited = new HashSet<>();
int[] result;
void dfs(Node from) {
if (from == null) {
from = idxToNode.get(initIdx);
visited.add(from);
// result.put(from.idx, -1);
result[from.idx-1]=-1;
}
for (Edge edge : from.nexts) {
Node next = edge.to;
// System.out.println(from.idx + "->" + next.idx);
if (next != from/* 防止走回头路 */&& !visited.contains(next)) {
visited.add(next);
// result.put(next.idx, from.idx);
result[next.idx-1]=from.idx;
dfs(next);
}
}
}
}
}01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8三种解法
- 暴力穷举
- 动态规划
- 贪心算法
贪心算法的错误尝试
import java.util.*;
public class _10_01背包问题 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();// 物品数
int V = sc.nextInt();// 背包容量
Item[] items = new Item[N];
for (int i = 0; i < N; i++) {
items[i] = new Item(sc.nextInt(), sc.nextInt());
}
sc.close();
// 思路是利用排序算法的稳定性来实现
Arrays.sort(items,(o1, o2) -> {
return Integer.compare(o1.weight, o2.weight);// 体积小的在前面
});
Arrays.sort(items,(o1, o2) -> {
return -Integer.compare(o1.value, o2.value);// 价值大的相对在前
});
System.out.println(Arrays.toString(items));
int valTotal = 0;
for(int i=0;i<items.length;i++) {
if(items[i].weight<=V) {
System.out.println(items[i]);
V-=items[i].weight;
valTotal+=items[i].value;
}
}
System.out.println(valTotal);
}
static class Item {
int weight, value;
public Item(int value, int weight) {
super();
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Item [weight=" + weight + ", value=" + value + "]";
}
}
}动态规划解法
dp[i][j] = 价值
表示,从物品0~i中任取,放到容量为j的背包中的最大价值import java.util.*;
public class _10_01背包问题_动态规划尝试 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();// 物品数
int V = sc.nextInt();// 背包容量
int[] values = new int[N];
int[] volume = new int[N];
for (int i = 0; i < N; i++) {
volume[i] = sc.nextInt();
values[i] = sc.nextInt();
}
sc.close();
// dp[把第i个物品][放入容量为j的背包的]=总价值
// dp[把第i个物品][放入容量为j的背包的]=dp[i-1][j-weight[i]]+value[i]
int[][] dp = new int[N][V + 1];
for (int j = 0; j < V + 1; j++) {
dp[0][j] = volume[0] <= j ? values[0] : 0;
}
int resMaxVal = 0;
for (int i = 1; i < N; i++) {
for (int j = 0; j < V + 1; j++) {
dp[i][j] = volume[i] <= j
? Math.max(dp[i - 1][j - volume[i]] + values[i], dp[i - 1][j])
: dp[i - 1][j];
if (dp[i][j] > resMaxVal) {
resMaxVal = dp[i][j];
}
}
}
System.out.println(resMaxVal);
}
}蛇形填数1

尝试版本1:有bug
输入
4
输出
[10, 11, 12, 1]
[9, 0, 13, 2]
[8, 15, 14, 3]
[7, 6, 5, 4]import java.util.*;
public class _11_蛇形填数 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
sc.close();
int[][] nums = new int[N][N];
int left=0,right=N-1,
top=0,bottom=N-1;
int y=0,x=N-1;
int num=1;
while(left<=right&&top<=bottom) {
while(y<bottom) nums[y++][x]=num++;
while(left<x) nums[y][x--]=num++;
while(top<y) nums[y--][x]=num++;
while(x<right-1) nums[y][x++]=num++;
top++;
left++;
right--;
bottom--;
}
for (int i = 0; i < nums.length; i++) {
System.out.println(Arrays.toString(nums[i]));
}
}
}尝试版本2:感觉是最优解了
输入
5
输出
[14, 15, 16, 17, 1]
[13, 25, 26, 18, 2]
[12, 24, 27, 19, 3]
[11, 23, 21, 20, 4]
[10, 8, 7, 6, 5]import java.util.*;
public class _11_蛇形填数 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
sc.close();
int[][] nums = new int[N][N];
int left=0,right=N-1,// 二维数组的最左侧、最右侧、最顶部、最底部
top=0,bottom=N-1;
int num=1;
while(left<=right&&top<=bottom) {
for(int y=top;y<=bottom;y++) {// 最左侧一列
nums[y][right]=num++;
}
for(int x=right-1;left<=x;x--) {// 最底部一行
nums[bottom][x]=num++;
}
for(int y=bottom;top+1<=y;y--) {// 最右侧一列
nums[y][left]=num++;
}
for(int x=left;x<=right-1;x++) {// 最顶部一行
nums[top][x]=num++;
}
left++;right--;// 缩小边框范围
top++;bottom--;
}
for (int i = 0; i < nums.length; i++) {
System.out.println(Arrays.toString(nums[i]));
}
}
}蛇形填数2
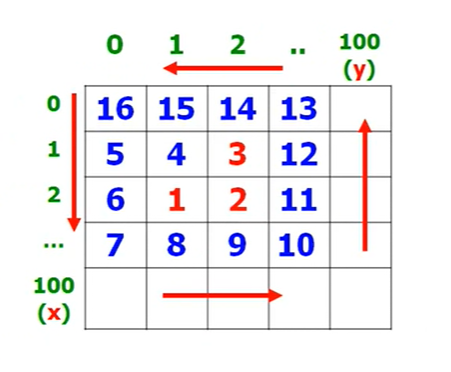
输入
4
输出
[16, 15, 14, 13]
[5, 4, 3, 12]
[6, 1, 2, 11]
[7, 8, 9, 10]import java.util.*;
public class _11_蛇形填数2 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
sc.close();
int[][] nums = new int[N][N];
int left=0,right=N-1,// 二维数组的最左侧、最右侧、最顶部、最底部
top=0,bottom=N-1;
int num=N*N;
while(left<=right&&top<=bottom) {
for(int x=left;x<=right;x++) {// 最顶部一行
nums[top][x]=num--;
}
for(int y=top+1;y<=bottom;y++) {// 最左侧一列
nums[y][right]=num--;
}
for(int x=right-1;left<=x;x--) {// 最底部一行
nums[bottom][x]=num--;
}
for(int y=bottom-1;top+1<=y;y--) {// 最右侧一列
nums[y][left]=num--;
}
left++;right--;// 缩小边框范围
top++;bottom--;
}
for (int i = 0; i < nums.length; i++) {
System.out.println(Arrays.toString(nums[i]));
}
}
}蛇形填数3

我的思路
对于左上角的数字,看成是填充矩阵的对角线,矩阵的宽分别为1,2,3,....N;
对于右下角的数字,看成是填充矩阵对角线,矩阵的宽度分别为 N-1,N-2,....1;,矩阵相对于填充数组的位置分别为 1,2,3,...N-1;
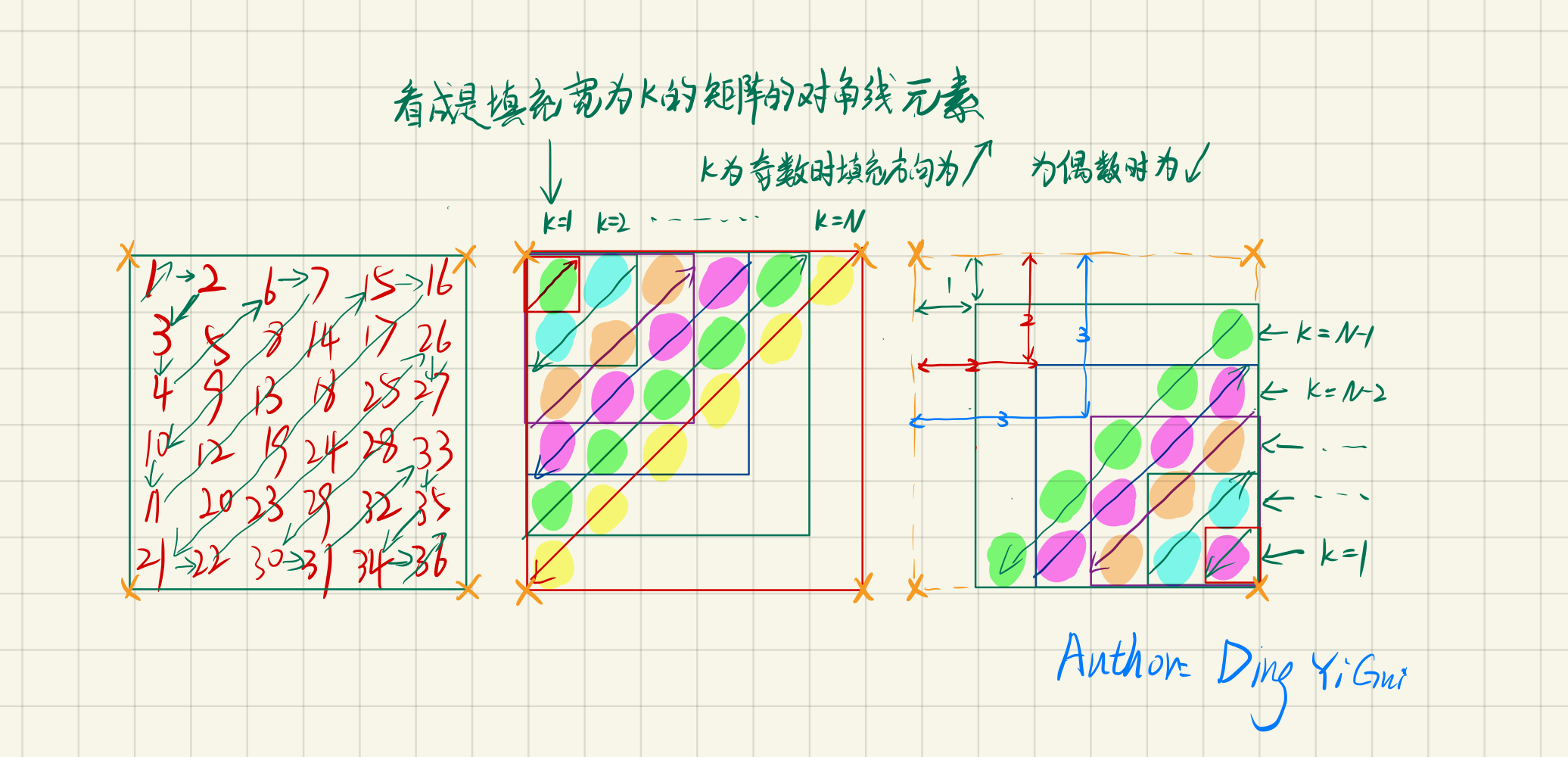
import java.util.*;
public class _11_蛇形填数3 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
sc.close();
int[][] nums = new int[N][N];
int num = 1;
int len=1;
while(len<=N) {
if(len%2==0) {// 方向不同
for (int i = 0; i < len; i++) {
nums[i][len-i-1]=num++;// 遍历矩阵对角线
}
}else {
for (int i = 0; i < len; i++) {
nums[len-i-1][i]=num++;// 遍历矩阵对角线
}
}
len++;
}
len=N-1;
int offset =1;
while(1<=len) {
if(len%2==0) {// 方向不同
for (int i = 0; i < len; i++) {
nums[offset+i][offset+len-i-1]=num++;// 遍历矩阵对角线,相对于原数组的偏移为offset
}
}else {
for (int i = 0; i < len; i++) {
nums[offset+len-i-1][offset+i]=num++;// 遍历矩阵对角线
}
}
offset++;
len--;
}
for (int i = 0; i < nums.length; i++) {
System.out.println(Arrays.toString(nums[i]));
}
}
}