SimpleFOC源码阅读学习笔记：快速反正切函数

丁毅桂大约 3 分钟

原理

这段SimpleFOC的代码实际来自开源项目ODrive的utils.cpp，

理论依据来自stackexchange中的一篇问答，

下面尝试记录对该函数的理解。

arctan2(z)的计算过程

参数化简：计算a := min (|x|, |y|) / max (|x|, |y|)，使得a∈[0,1]。
多项式逼近：使用一个多项式来近似计算 arctan(a) 的值。
结果调整：根据x和y的正负性来判断实际所在的象限，计算实际的arctan2(a)角度

计算反正切

这里使用的是一个多项式计算反正切，该多项式是对arctan()函数的一种逼近

泰勒级数展开（Taylor Series Expansion）逼近

泰勒级数是一种常用的数学工具，
其更多地关注函数在某一点附近的局部函数值
随着 $x$ 的增大，泰勒级数的误差可能会增加。
对于 $\arctan(x)$ 函数，它的泰勒级数在 $x=0$ 处展开为：
$\arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots$

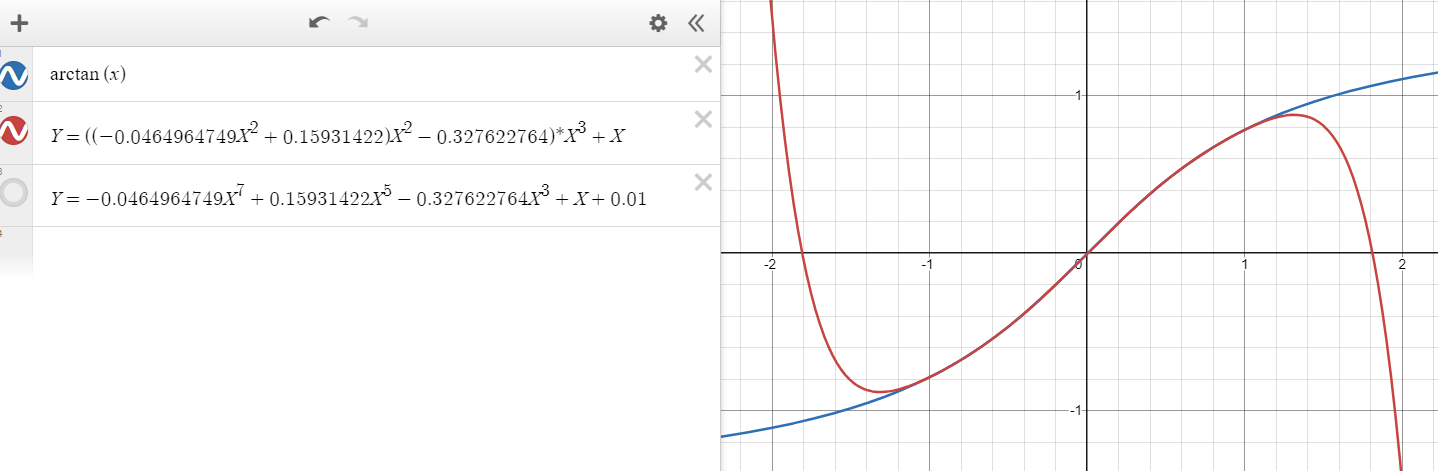
最小最大值逼近（minimax approximation）

这种方法的目标是在给定区间（如[0,1]）内找到一个多项式，使得该多项式与目标函数之间的最大偏差最小化。这样的多项式函数图像在整体上更接近目标函数图像。
对于 $\arctan(x)$ 函数，在给定区间[0,1]通过雷米兹（Remez）算法确定的最佳系数为：
$\arctan(x) = -0.0464964749 x^7 +0.15931422 x^5 - 0.327622764 x^3 + x$

多项式化简

这里使用霍纳法则来对多项式进行化简，目的是减少计算机计算乘法的次数。

原理是拆分多项式，如:

$y=Ax^4+Bx^3+Cx^2+Dx^1$

该多项式至少需要计算(0+1)+(1+1)+(1+1)+(1+1)=7次乘法

而将其拆分得到：

$y=x(D+x(C+x(B+A(x))))$

该多项式只需要计算4次乘法

所以

这里可以把：-0.0464964749 x^7 +0.15931422 x^5 - 0.327622764 x^3 + x

写成：((-0.0464964749fx^2 + 0.15931422f)x^2 - 0.327622764f)x^3 + x

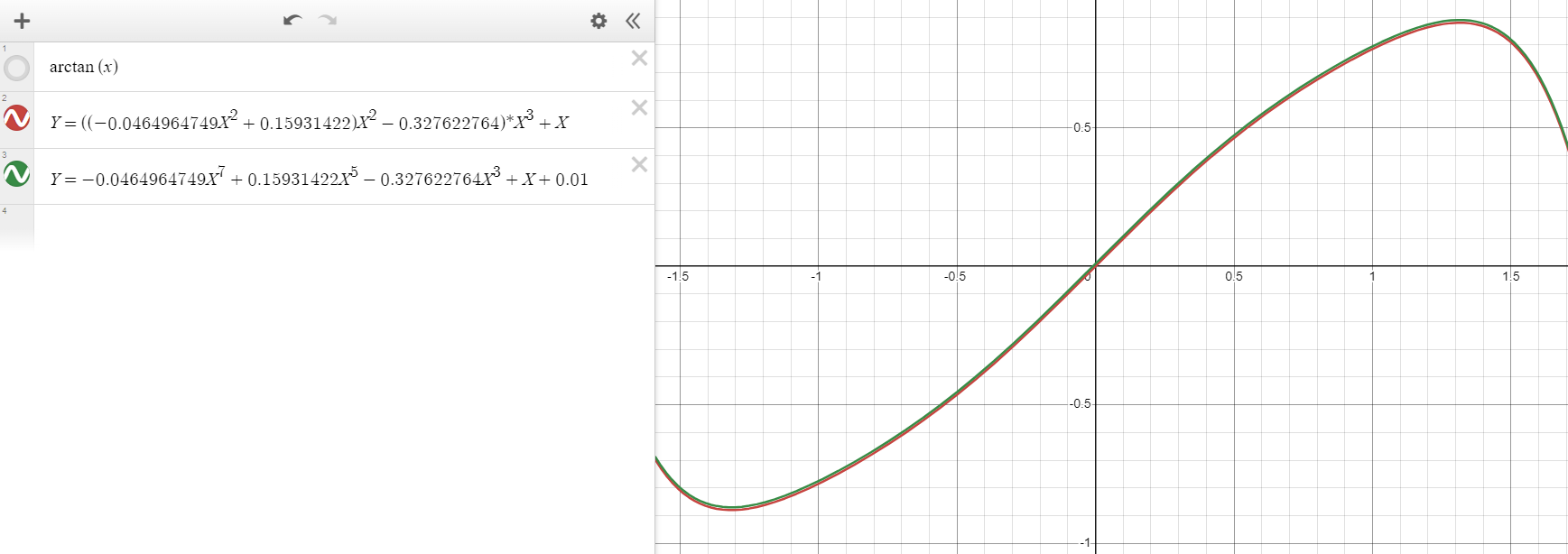
// s := a * a
float s = a * a;
// r := ((-0.0464964749 * s + 0.15931422) * s - 0.327622764) * s * a + a
float r = ((-0.0464964749f * s + 0.15931422f) * s - 0.327622764f) * s * a + a;

根据(x,y)所在象限计算arctan2

下面的1.57079637f为90° 3.14159274f为180°

如果abs_y > abs_x那么上面实际计算的是arctan(a=x/y)，
否则，实际计算的是arctan(a=y/z)

根据公式：arctan(z)=π/2−arctan(1/z)
所以r = 1.57079637f - r

// if |y| > |x| then r := 1.57079637 - r
if (abs_y > abs_x) r = 1.57079637f - r;

x<0 可以认为是将r从第一或四象限翻转到第二或三象限：

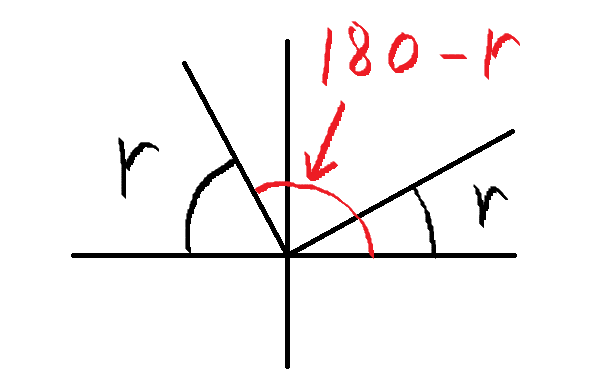
// if x < 0 then r := 3.14159274 - r
if (x < 0.0f) r = 3.14159274f - r;

y<0 可以认为是将r从第一或二象限翻转到第三或四象限：

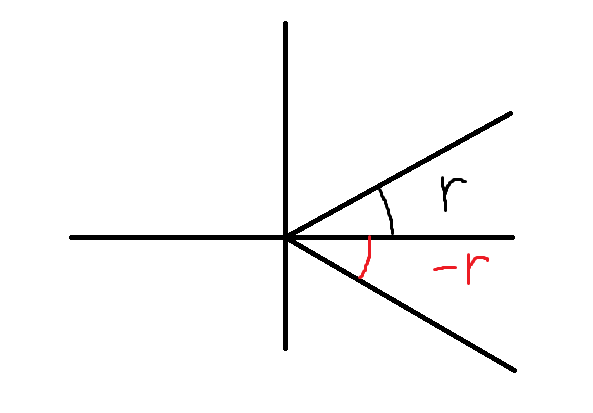
// if y < 0 then r := -r
if (y < 0.0f) r = -r;

源代码

#include "foc_utils.h"
// fast_atan2 based on https://math.stackexchange.com/a/1105038/81278
// Via Odrive project
// https://github.com/odriverobotics/ODrive/blob/master/Firmware/MotorControl/utils.cpp
// This function is MIT licenced, copyright Oskar Weigl/Odrive Robotics
// The origin for Odrive atan2 is public domain. Thanks to Odrive for making
// it easy to borrow.
__attribute__((weak)) float _atan2(float y, float x) {
    // a := min (|x|, |y|) / max (|x|, |y|)
    float abs_y = fabsf(y);
    float abs_x = fabsf(x);
    // inject FLT_MIN in denominator to avoid division by zero
    float a = min(abs_x, abs_y) / (max(abs_x, abs_y));
    // s := a * a
    float s = a * a;
    // r := ((-0.0464964749 * s + 0.15931422) * s - 0.327622764) * s * a + a
    float r =
        ((-0.0464964749f * s + 0.15931422f) * s - 0.327622764f) * s * a + a;
    // if |y| > |x| then r := 1.57079637 - r
    if (abs_y > abs_x) r = 1.57079637f - r;
    // if x < 0 then r := 3.14159274 - r
    if (x < 0.0f) r = 3.14159274f - r;
    // if y < 0 then r := -r
    if (y < 0.0f) r = -r;

    return r;
  }