SimpleFOC源码阅读学习笔记:查表法计算正弦余弦值
2024/9/6大约 3 分钟
作用
源代码中称,使用这种方法计算正弦余弦后,计算耗时从300us降低到了110us,性能提升了3倍。
BLDCMotor.cpp
// Function using sine approximation
// regular sin + cos ~300us (no memory usage)
// approx _sin + _cos ~110us (400Byte)
void BLDCMotor::setPhaseVoltage(float Uq, float Ud, float angle_el) {
......
}原理
foc_utils.c中的代码实现了一个简化版的正弦函数计算方法,它使用了一个包含65个元素的查找表(lookup table)来进行近似计算,并通过线性插值来提高精度。这种方法在资源受限的环境中非常有用,比如在嵌入式系统中,可以节省大量的计算资源。
下面是对代码的一些理解和解释:
sine_array 是一个16位整数数组,存储了1/4个周期内的正弦值。
剩下3/4周期的sin值和前1/4周期对称(左右对称、上下对称、原点对称),不需要存储
数组本身的精度应该是90°/64=1.406°,经过线性插值精度将会更高。
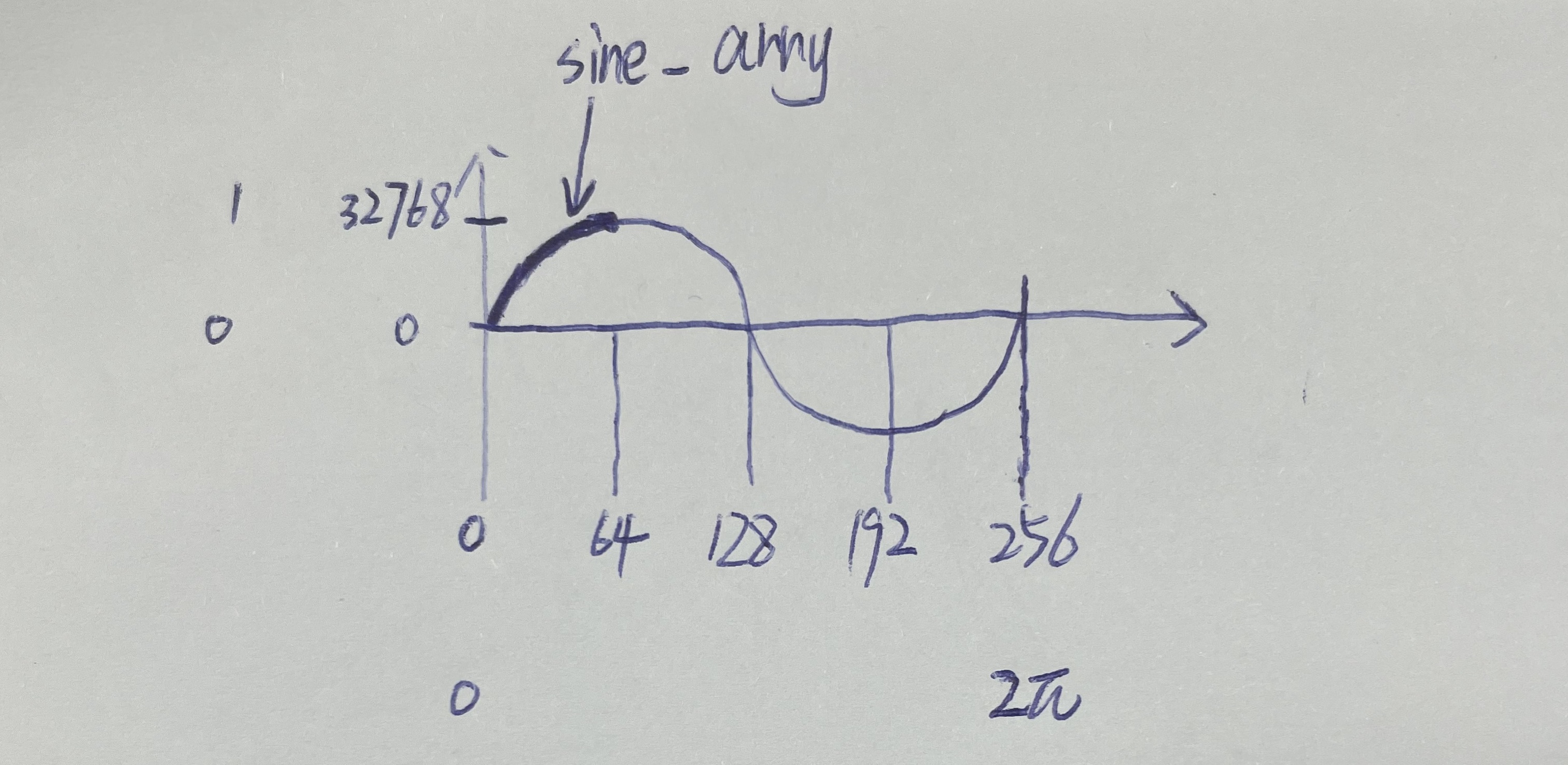
static uint16_t sine_array[65] = {0,804,1608,2411,3212,4011,4808,5602,6393,7180,7962,8740,9512,10279,11039,11793,12540,13279,14010,14733,15447,16151,16846,17531,18205,18868,19520,20160,20788,21403,22006,22595,23170,23732,24279,24812,25330,25833,26320,26791,27246,27684,28106,28511,28899,29269,29622,29957,30274,30572,30853,31114,31357,31581,31786,31972,32138,32286,32413,32522,32610,32679,32729,32758,32768};i = (unsigned int)(a * (64*4*256.0f/_2PI)); 是计算索引,可以拆分两部分
i=a*64*4/_2PI实现将a从[0,2PI]映射到[0,256]i*=256.0f实现将i放大2^8=256倍,即把二进制小数点往左移动8位。
unsigned int i = (unsigned int)(a * (64*4*256.0f/_2PI));frac = i & 0xff 得到小数部分i = (i >> 8) & 0xff 得到整数部分
int frac = i & 0xff;
i = (i >> 8) & 0xff;根据所在的周期计算值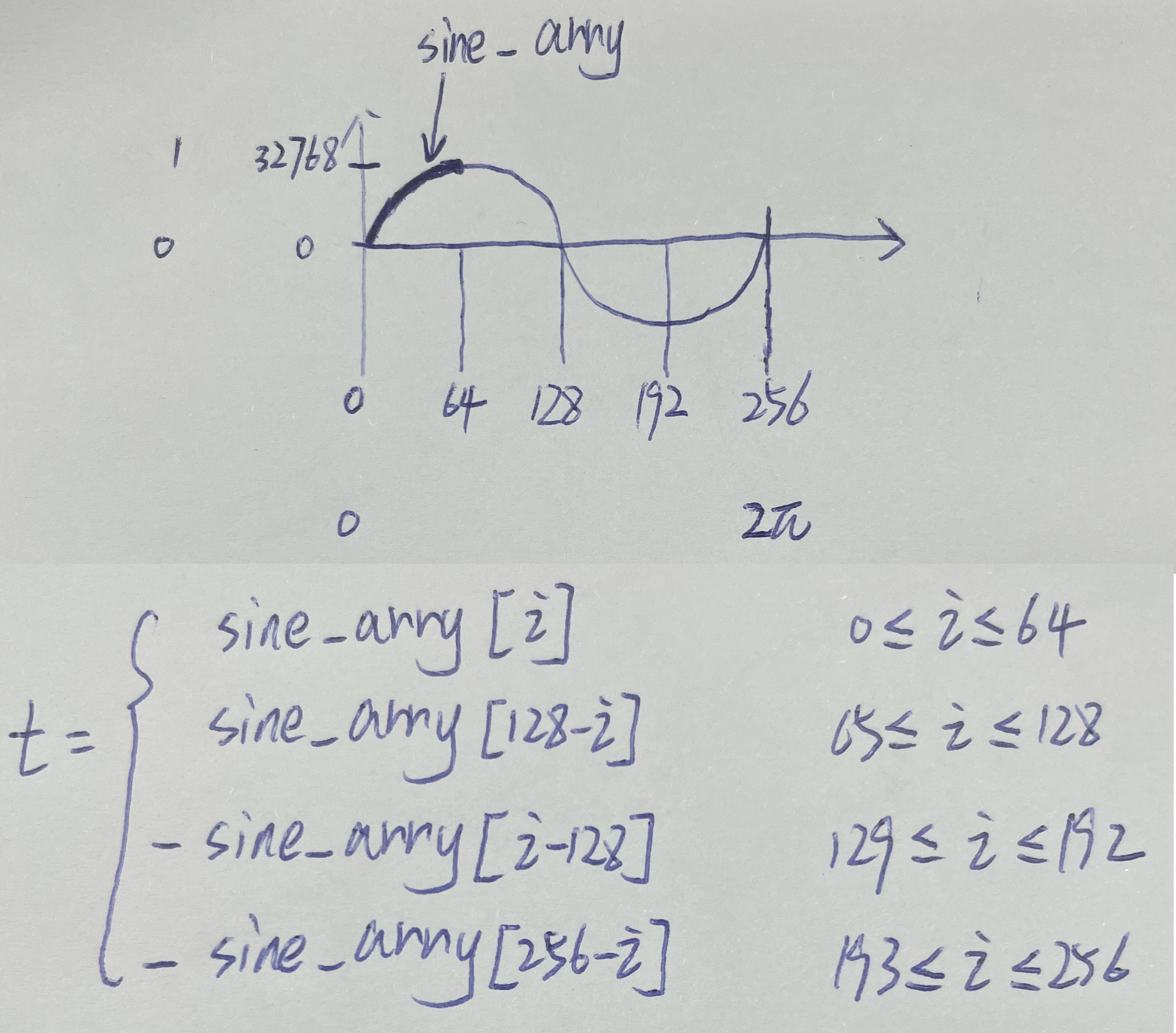
if (i < 64) {
t1 = (int32_t)sine_array[i]; t2 = (int32_t)sine_array[i+1];
}
else if(i < 128) {
t1 = (int32_t)sine_array[128 - i]; t2 = (int32_t)sine_array[127 - i];
}
else if(i < 192) {
t1 = -(int32_t)sine_array[-128 + i]; t2 = -(int32_t)sine_array[-127 + i];
}
else {
t1 = -(int32_t)sine_array[256 - i]; t2 = -(int32_t)sine_array[255 - i];
}通过线性插值来提高精度
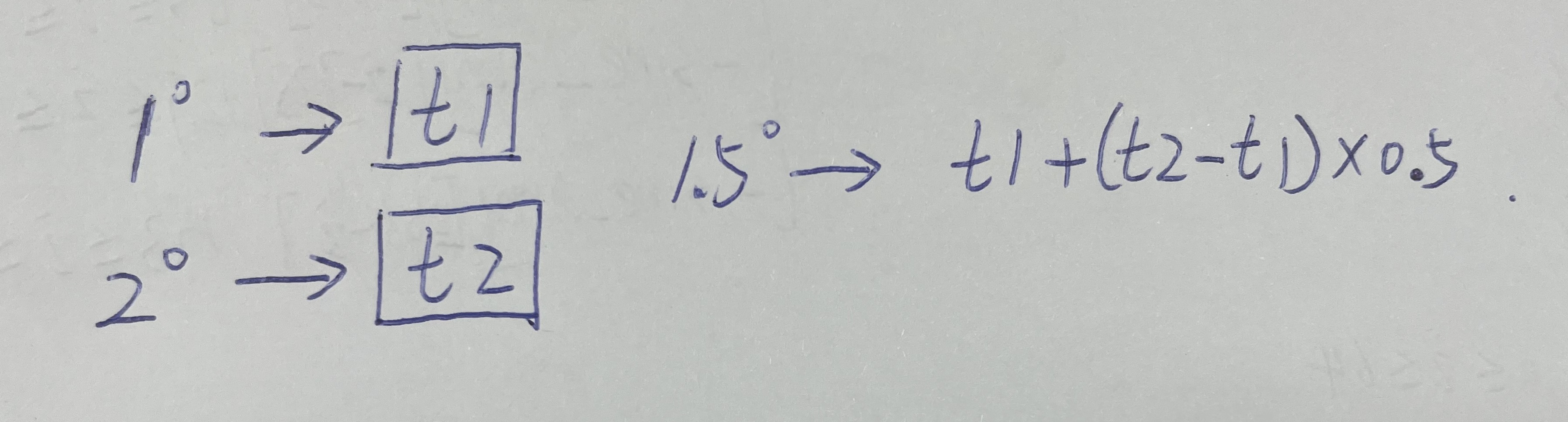
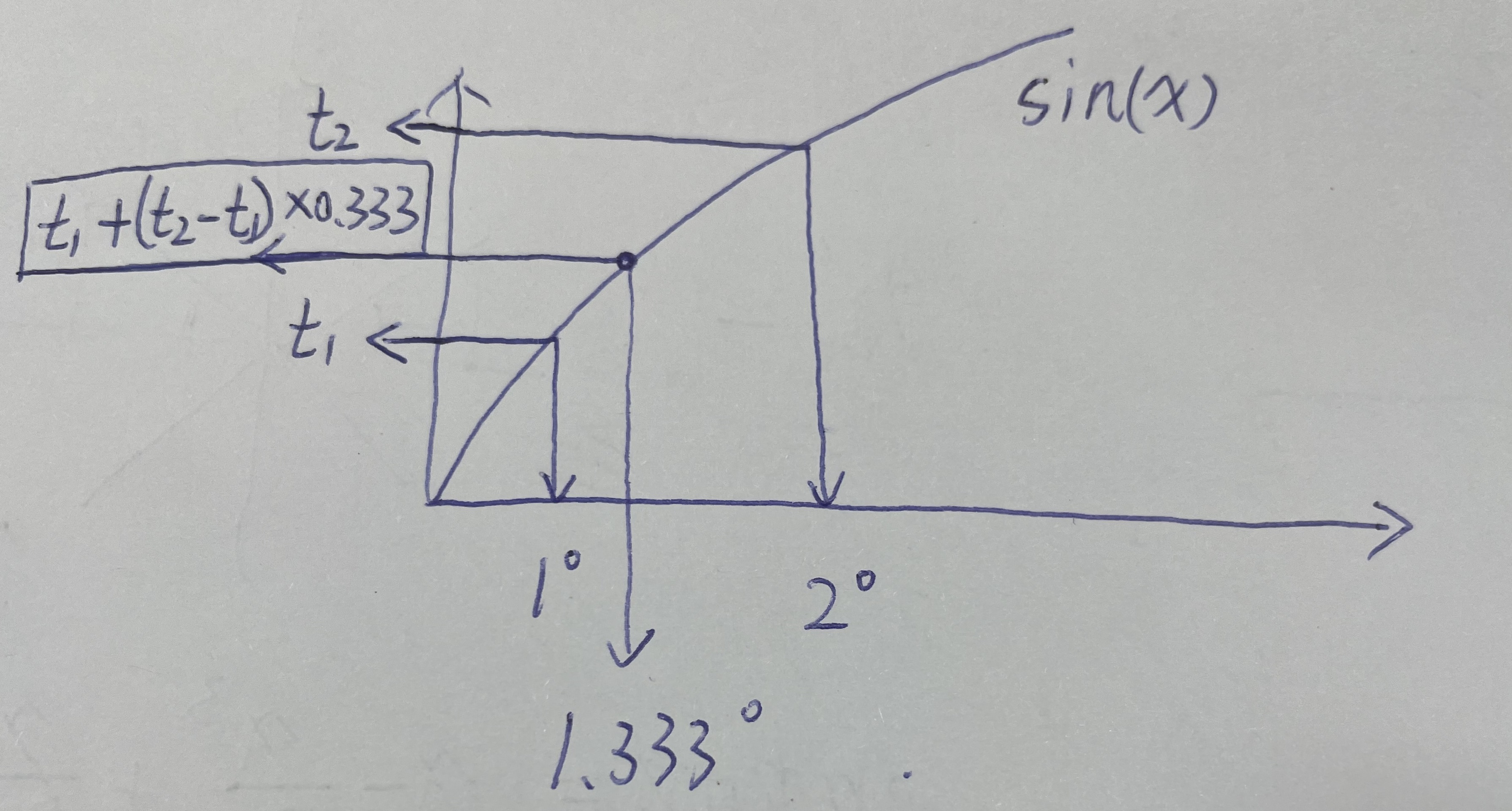
return (1.0f/32768.0f) * (t1 + (((t2 - t1) * frac) >> 8));cos函数可用通过sin函数求解,
因为在其图像上,sin向左平移π/2就是cos
sin(π/2 + x) = cos(x)
唯一可能需要注意的只有定义域的范围,须保证 a_sin∈[0,2PI]
float _cos(float a){
float a_sin = a + _PI_2;
a_sin = a_sin > _2PI ? a_sin - _2PI : a_sin;
return _sin(a_sin);
}源代码
#include "foc_utils.h"
// function approximating the sine calculation by using fixed size array
// uses a 65 element lookup table and interpolation
// thanks to @dekutree for his work on optimizing this
__attribute__((weak)) float _sin(float a){
// 16bit integer array for sine lookup. interpolation is used for better precision
// 16 bit precision on sine value, 8 bit fractional value for interpolation, 6bit LUT size
// resulting precision compared to stdlib sine is 0.00006480 (RMS difference in range -PI,PI for 3217 steps)
static uint16_t sine_array[65] = {0,804,1608,2411,3212,4011,4808,5602,6393,7180,7962,8740,9512,10279,11039,11793,12540,13279,14010,14733,15447,16151,16846,17531,18205,18868,19520,20160,20788,21403,22006,22595,23170,23732,24279,24812,25330,25833,26320,26791,27246,27684,28106,28511,28899,29269,29622,29957,30274,30572,30853,31114,31357,31581,31786,31972,32138,32286,32413,32522,32610,32679,32729,32758,32768};
int32_t t1, t2;
unsigned int i = (unsigned int)(a * (64*4*256.0f/_2PI));
int frac = i & 0xff;
i = (i >> 8) & 0xff;
if (i < 64) {
t1 = (int32_t)sine_array[i]; t2 = (int32_t)sine_array[i+1];
}
else if(i < 128) {
t1 = (int32_t)sine_array[128 - i]; t2 = (int32_t)sine_array[127 - i];
}
else if(i < 192) {
t1 = -(int32_t)sine_array[-128 + i]; t2 = -(int32_t)sine_array[-127 + i];
}
else {
t1 = -(int32_t)sine_array[256 - i]; t2 = -(int32_t)sine_array[255 - i];
}
return (1.0f/32768.0f) * (t1 + (((t2 - t1) * frac) >> 8));
}
// function approximating cosine calculation by using fixed size array
// ~55us (float array)
// ~56us (int array)
// precision +-0.005
// it has to receive an angle in between 0 and 2PI
__attribute__((weak)) float _cos(float a){
float a_sin = a + _PI_2;
a_sin = a_sin > _2PI ? a_sin - _2PI : a_sin;
return _sin(a_sin);
}
__attribute__((weak)) void _sincos(float a, float* s, float* c){
*s = _sin(a);
*c = _cos(a);
}