FOC算法学习与实现笔记-02.帕克变换

帕克变换

• 实际上，完成帕克变换后得到的d和q值，描述的是施加在转子上的磁场（力矩和方向），
• 并且这个磁场方向一般垂直于d轴，即$i_d=0$
• 这是为了确保所有电流都产生转矩，而不是增强或减小定子上永磁体的磁场。

• 克拉克变换就是把坐标轴固定在了转子上，
• 然后只关注施加在转子上的磁场（大小和方向），
• 不关注定子内的磁场（大小和方向）。
• 具体做法就是创建一个固定在转子上的坐标轴，
• 然后通过转子的磁场（大小和方向）和测量出的转子和定子的夹角，
• 就能计算出定子施加在转子上的磁场（大小和方向）

dq坐标系

• 建立一个dq坐标系,将其固定在定子上
• 

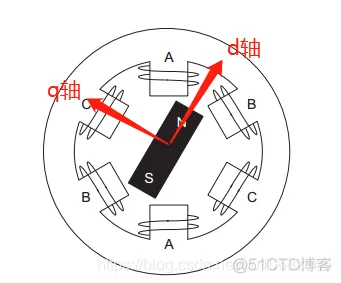
坐标轴旋转

• 通过定子（α-β坐标轴）上的磁场（F）
• 以及定子（α-β坐标轴）和转子（d-q坐标轴）的夹角（φ）
• 计算作用在转子（d-q坐标轴）上的磁场(F)
• 

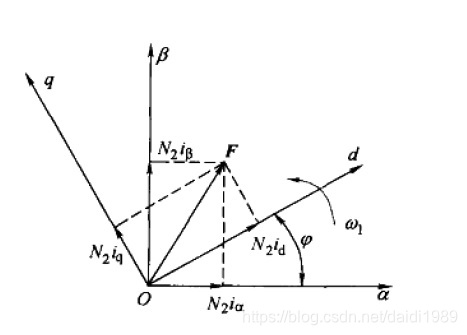
基本形式推导

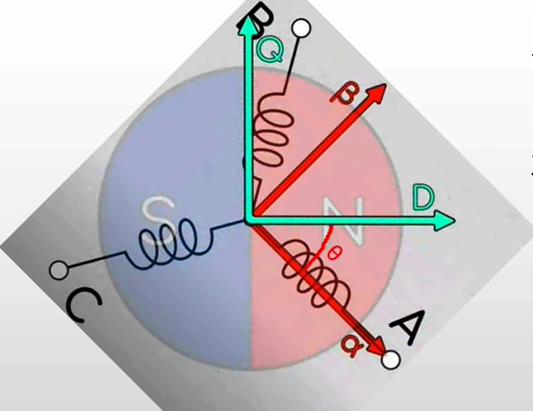
• Iα
  • 作用在D轴上的量 = Iα cos(θ)
  • 作用在Q轴上的量 = Iα -sin(θ)
• Iβ
  • 作用在D轴上的量 = Iβ sin(θ)
  • 作用在Q轴上的量 = Iβ cos(θ)

$$I_d = I_α \cos{θ} + I_β \sin{θ} \\ I_q = - I_α \sin{θ} + I_β \cos{θ} \\$$

$$\left[ \begin{matrix} I_d \\ I_q \end{matrix} \right] = \left[ \begin{matrix} \cos{θ} & \sin{θ} \\ -\sin{θ} & \cos{θ} \end{matrix} \right] \left[ \begin{matrix} I_α \\ I_β \end{matrix} \right]$$

系数矩阵实际是一个旋转矩阵，
它实现了将两相静止坐标系 (α, β) 中的向量转换到同步旋转坐标系 (d, q) 中。

基本形式的逆变换

由于系数矩阵是一个正交矩阵（旋转矩阵），它的逆矩阵实际上就是它的转置矩阵。对于正交矩阵来说，转置等于逆矩阵，这是因为旋转矩阵的行列式为 1，而且其列向量之间相互正交。

因此，上述矩阵的逆变换（即从 (d, q) 坐标系回到 (α, β) 坐标系）可以表示为原矩阵的转置：

$$\begin{bmatrix} I_\alpha \\ I_\beta \end{bmatrix} = \begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix} \begin{bmatrix} I_d \\ I_q \end{bmatrix}$$