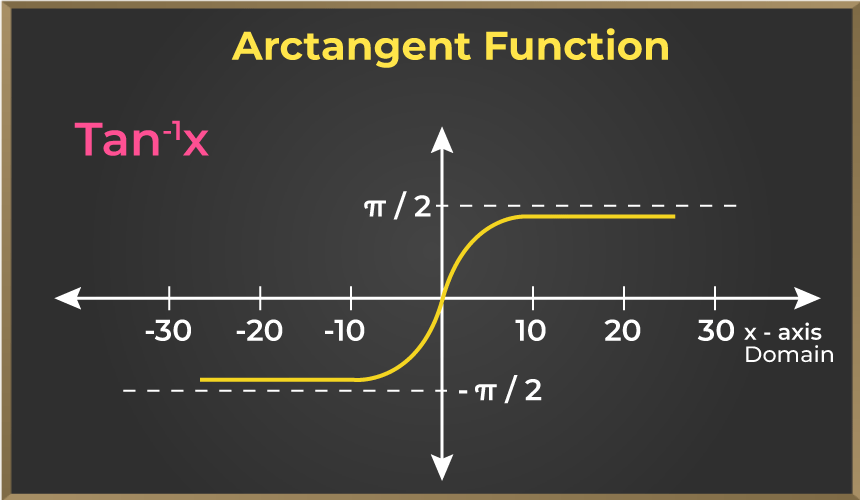
FOC算法学习与实现笔记-04.高频方波注入提取位置公式推导

高频方波注入提取位置公式推导

• 作用
  • 可以在电机d轴（或估计的d轴）注入高频方波，
  • 然后通过提取电流响应信号，
  • 来估算电机转子的角度。
• 方法
  • 把pwm信号的两个周期作为高频方波信号的周期
  • 往电机的D轴注入电压信号
  • 在方波的上半个周期注入正电压，
  • 在方波的下半个周期注入负电压。

dq轴电压、电流方程

$$\begin{align*} U_d &= RI_d + L_d \frac{d}{dt}I_d - \omega_e L_q I_q \\ U_q &= RI_q + L_q \frac{d}{dt}I_q - \omega_e L_d I_d + \omega_e \psi_f \\ \end{align*}$$

简化模型

• 当注入高频电压时，感抗电压远远大于电阻和磁链的压降，
• 所以电阻和磁链上的电压响应可以忽略不计

$$U_d = L_d \frac{d}{dt}I_d \\ U_q = L_q \frac{d}{dt}I_q \\$$

写成矩阵形式

$$\begin{bmatrix} U_d \\ U_q \\ \end{bmatrix} = \begin{bmatrix} L_d \frac{d}{dt} & 0\\ 0 & L_q \frac{d}{dt} \\ \end{bmatrix} \begin{bmatrix} I_d \\ I_q \\ \end{bmatrix}$$

写成电流方程

$$\begin{bmatrix} I_d \\ I_q \\ \end{bmatrix} = \begin{bmatrix} L_d \frac{d}{dt} & 0\\ 0 & L_q \frac{d}{dt} \\ \end{bmatrix}^{-1} \begin{bmatrix} U_d \\ U_q \\ \end{bmatrix}$$

旋转到α-β轴（帕克逆变换）

$$\begin{bmatrix} I_\alpha \\ I_\beta \\ \end{bmatrix} = \begin{bmatrix} \cos{θ} & \sin{θ} \\ -\sin{θ} & \cos{θ} \end{bmatrix}^{-1} \begin{bmatrix} L_d \frac{d}{dt} & 0\\ 0 & L_q \frac{d}{dt} \\ \end{bmatrix}^{-1} \begin{bmatrix} U_d \\ U_q \\ \end{bmatrix}$$

用估计d-q坐标轴电压，表示真实d-q坐标轴电压

• $\hat{d}$ 是估计的d轴
• $θ_e$ 是d轴的实际位置
• $\hat{θ_e}$是d轴的估计位置
• $\tilde{θ_e}=θ_e-\hat{θ_e}$ 是d轴实际位置和估计位置的误差
• 

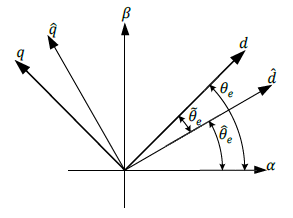
通过帕克变换，就能使用角度误差 $\tilde{θ_e}$ 和 估计的d-q轴 来表示 真实的d-q轴。

$$\begin{bmatrix} U_d \\ U_q \\ \end{bmatrix} = \begin{bmatrix} \cos{\tilde{θ_e}} & \sin{\tilde{θ_e}} \\ -\sin{\tilde{θ_e}} & \cos{\tilde{θ_e}} \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ \hat{U_q} \\ \end{bmatrix}$$

代入之前推导出的关系式，
就能得到 估计d-q轴高频电压激励 和 真实α-β轴的高频电流响应 的关系式 。

$$\begin{bmatrix} I_\alpha \\ I_\beta \\ \end{bmatrix} = \begin{bmatrix} \cos{θ} & \sin{θ} \\ -\sin{θ} & \cos{θ} \end{bmatrix}^{-1} \begin{bmatrix} L_d \frac{d}{dt} & 0\\ 0 & L_q \frac{d}{dt} \\ \end{bmatrix}^{-1} \begin{bmatrix} \cos{\tilde{θ_e}} & \sin{\tilde{θ_e}} \\ -\sin{\tilde{θ_e}} & \cos{\tilde{θ_e}} \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ \hat{U_q} \\ \end{bmatrix}$$

化简：计算逆矩阵

• 旋转矩阵的逆就是其转置矩阵
• 对角矩阵的逆就是把对角元素取倒数

$$\begin{bmatrix} I_\alpha \\ I_\beta \\ \end{bmatrix} = \begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix} \begin{bmatrix} \frac{1}{L_d \frac{d}{dt}} & 0\\ 0 & \frac{1}{L_q \frac{d}{dt}} \\ \end{bmatrix} \begin{bmatrix} \cos{\tilde{θ_e}} & \sin{\tilde{θ_e}} \\ -\sin{\tilde{θ_e}} & \cos{\tilde{θ_e}} \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ \hat{U_q} \\ \end{bmatrix}$$

化简：计算矩阵乘法

$$\begin{bmatrix} I_\alpha \\ I_\beta \\ \end{bmatrix} = \begin{bmatrix} \frac{\cos{\theta}}{L_d \frac{d}{dt}} & \frac{-\sin{\theta}}{L_q \frac{d}{dt}}\\ \frac{\sin{\theta}}{L_d \frac{d}{dt}} & \frac{\cos{\theta}}{L_q \frac{d}{dt}}\\ \end{bmatrix} \begin{bmatrix} \cos{\tilde{θ_e}} & \sin{\tilde{θ_e}} \\ -\sin{\tilde{θ_e}} & \cos{\tilde{θ_e}} \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ \hat{U_q} \\ \end{bmatrix}$$

化简：假设估计的dq轴位置就是实际dq轴的位置

• 由于估计的dq轴和实际dq轴的误差角度在迭代多次后逐渐逼近0，
• 这将导致旋转矩阵变成单位矩阵
• 也就是假设估计的dq轴位置就是实际dq轴的位置。

$$\begin{align*} \begin{bmatrix} I_\alpha \\ I_\beta \\ \end{bmatrix} &= \begin{bmatrix} \frac{\cos{\theta}}{L_d \frac{d}{dt}} & \frac{-\sin{\theta}}{L_q \frac{d}{dt}}\\ \frac{\sin{\theta}}{L_d \frac{d}{dt}} & \frac{\cos{\theta}}{L_q \frac{d}{dt}}\\ \end{bmatrix} \begin{bmatrix} \cos{\tilde{θ_e}} & \sin{\tilde{θ_e}} \\ -\sin{\tilde{θ_e}} & \cos{\tilde{θ_e}} \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ \hat{U_q} \\ \end{bmatrix} \\ &= \begin{bmatrix} \frac{\cos{\theta}}{L_d \frac{d}{dt}} & \frac{-\sin{\theta}}{L_q \frac{d}{dt}}\\ \frac{\sin{\theta}}{L_d \frac{d}{dt}} & \frac{\cos{\theta}}{L_q \frac{d}{dt}}\\ \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ \hat{U_q} \\ \end{bmatrix} \\ &= \begin{bmatrix} \frac{\cos{\theta}}{L_d \frac{d}{dt}} & \frac{-\sin{\theta}}{L_q \frac{d}{dt}}\\ \frac{\sin{\theta}}{L_d \frac{d}{dt}} & \frac{\cos{\theta}}{L_q \frac{d}{dt}}\\ \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ \hat{U_q} \\ \end{bmatrix} \end{align*}$$

化简：注入q轴的电压为0

• 由于我们通常只在估计的d-q轴的d轴注入高频电压，
• 所以注入q轴的电压为0，

$$\begin{align*} \begin{bmatrix} I_\alpha \\ I_\beta \\ \end{bmatrix} &= \begin{bmatrix} \frac{\cos{\theta}}{L_d \frac{d}{dt}} & \frac{-\sin{\theta}}{L_q \frac{d}{dt}}\\ \frac{\sin{\theta}}{L_d \frac{d}{dt}} & \frac{\cos{\theta}}{L_q \frac{d}{dt}}\\ \end{bmatrix} \begin{bmatrix} \hat{U_d} \\ 0 \\ \end{bmatrix}\\ &= \begin{bmatrix} \frac{\cos{\theta}}{L_d \frac{d}{dt}}\\ \frac{\sin{\theta}}{L_d \frac{d}{dt}}\\ \end{bmatrix} \hat{U_d}\\ &= \frac{\hat{U_d}}{L_d \frac{d}{dt}} \begin{bmatrix} \cos{\theta}\\ \sin{\theta}\\ \end{bmatrix} \end{align*}$$

求出角度

$$\begin{align*} \tan\theta &= \frac{\sin\theta}{\cos\theta} = \frac{I_\beta}{I_\alpha} \\ \theta &= \arctan(\frac{I_\beta}{I_\alpha}) \end{align*}$$

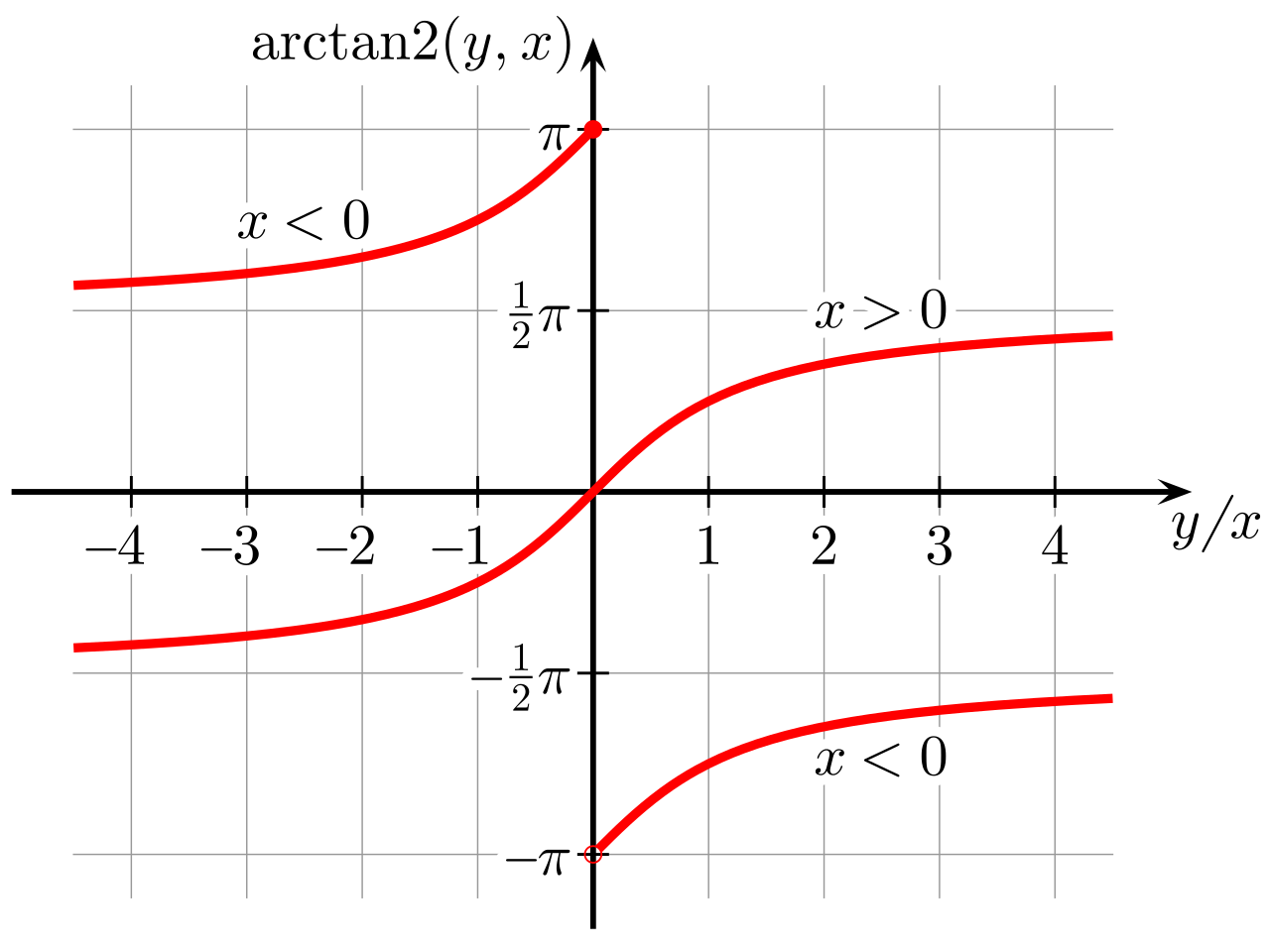
改为使用atan2(a,b)计算角度

$$\theta = \text{atan2}(I_\beta,I_\alpha)$$

• 因为$\tan(\frac{a}{b})$只能计算出$[-\frac{\pi}{2},\frac{\pi}{2}]$范围的角度,并且无法处理分母为0的情况。
  • 
• 所以这里需要使用 $\text{atan2}(a,b)$ 其可以计算出 $(-\pi,\pi]$ 范围的角度。
  • 

参考

无感FOC之高频注入法——永磁同步电机控制 https://aijishu.com/a/1060000000315769