电容电感
2024/12/9大约 4 分钟
电容电感
电容Capacitors
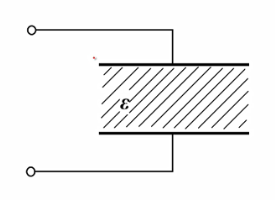
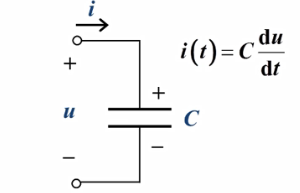
关于电容定义式的推导需要电磁场的知识,暂时不了解,跳过,以后再说
- 定义式:
- 单位: F法
- 注意:
- C与q和u无关,C只和介电常数ε、极板面积s、两极板之间距离d有关。
- 类比于电阻:R=u/i但R与u和i无关,R只和导体的材质、横截面积等因素有关。
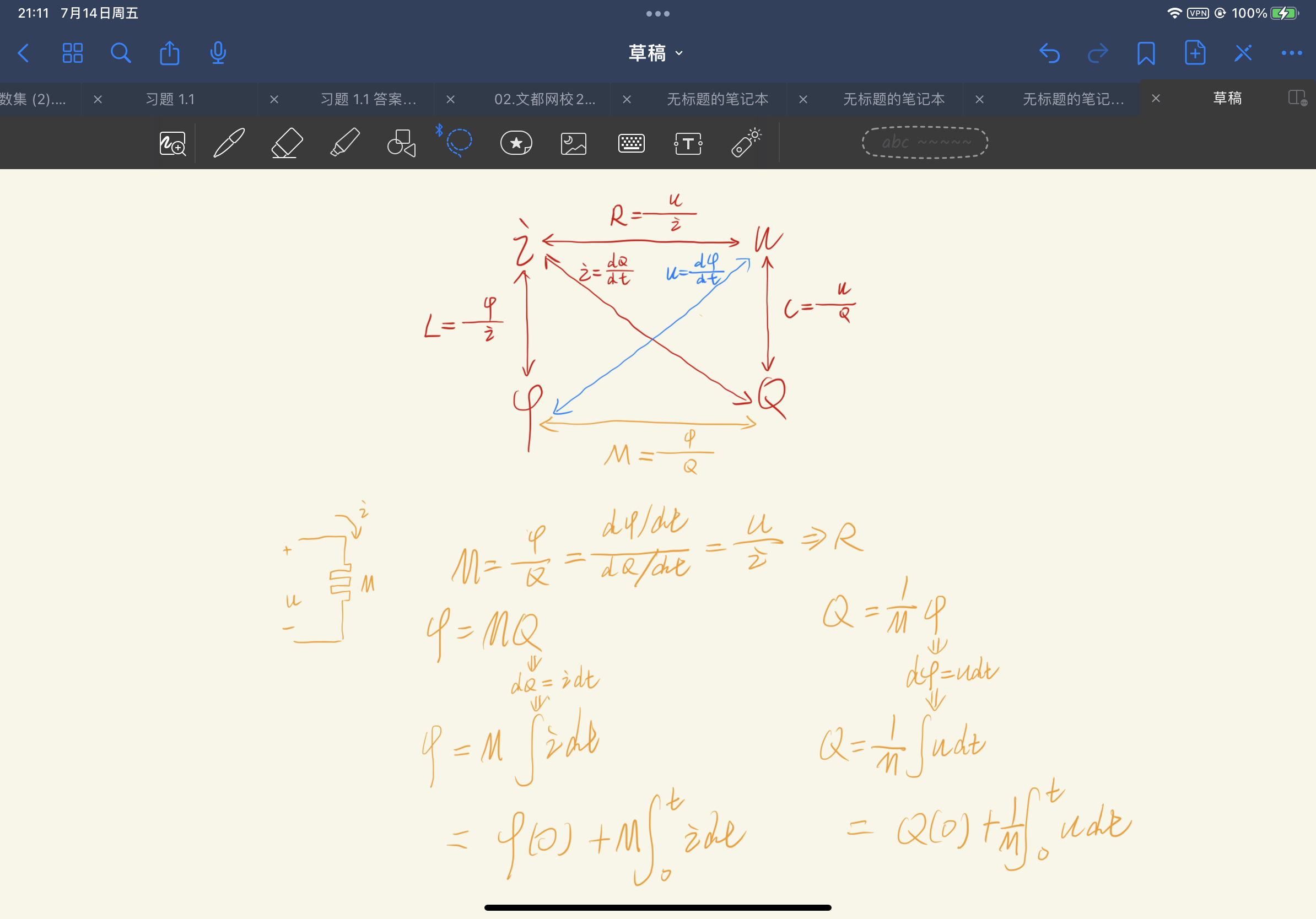
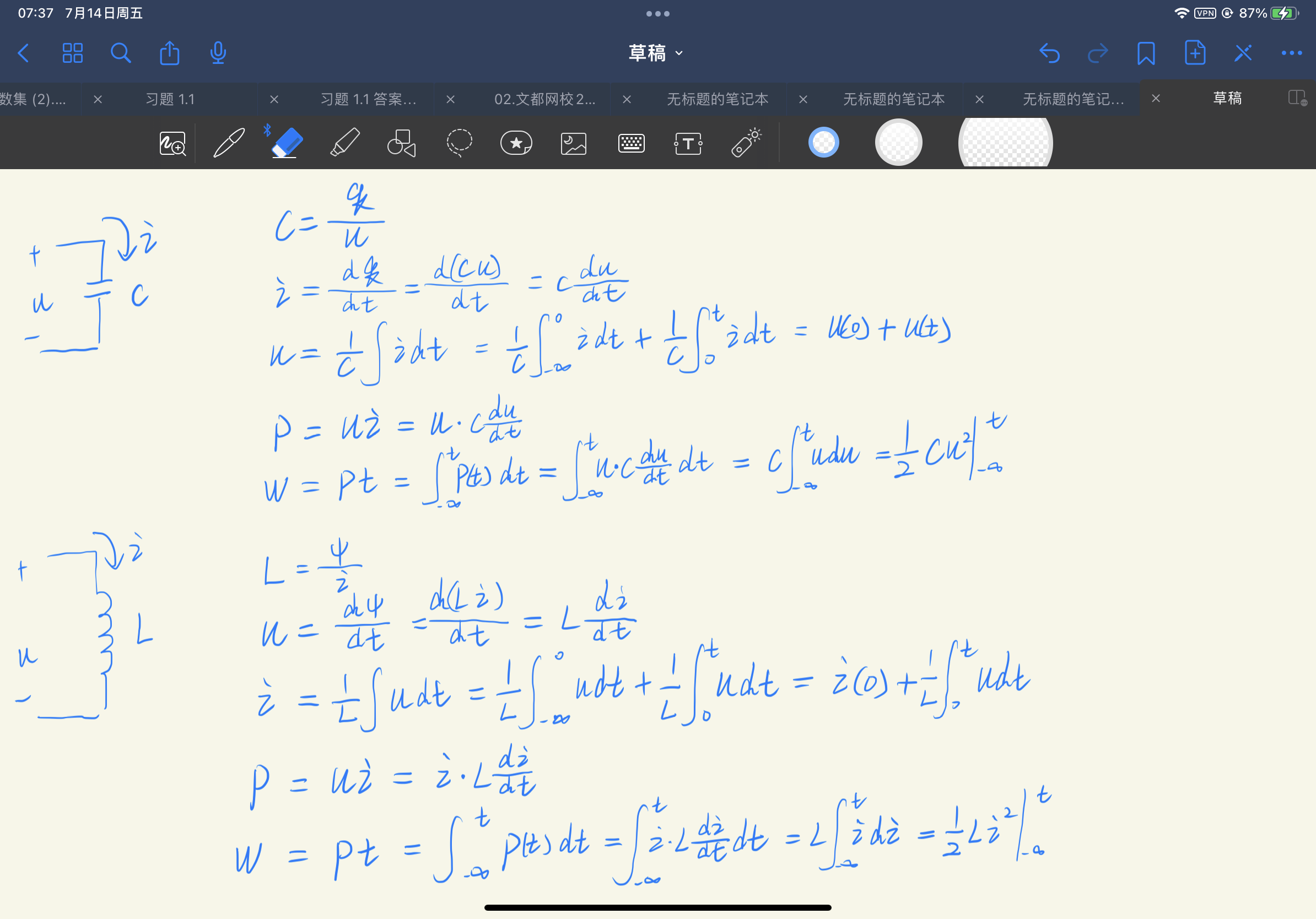
- 其上电流公式的推导:
- 由于:
- 所以:
- 由于:
- 所以电容上电流为
- 所以可以认为:电容上的电流=C乘上电压的变化率(导数)。
- 由于:
- 其上电压公式的推导:
- 由于:
- 所以:
- 所以:
- 所以:
- 这里似乎都会把微分的dt写成dτ,原因应该是为了区分其不同的含义
- 所以:
- 所以:
- 所以可以认为:t时刻电容上的电压=0时刻的其上的电压+
- 由于:
- 吸收的功率
- 吸收的能量
- 所以:
- 注意:
- 这里还可以写成
- 即t时刻吸收的能量=-∞到t0时刻吸收的能量 + t0到t时刻吸收的能量
- 从而可以推出t0时刻到t时刻的能量变化,就是W(t0) 到 W(t) 能量的变化
- 这里还可以写成
- 注意:
- 所以:
- u可以是一个常数,也可以是t的函数,
- 显然,u是常数时,吸收的能量为0
- 所以:
- 可以认为-∞时刻吸收的功率为0
- 则:
- 简写:
t0->t时刻的电容的能量变化:
- 简写:
- 另外:
- 由于:
- 所以带入可得:
- 由于Q是>=0的,所以
- 由于:
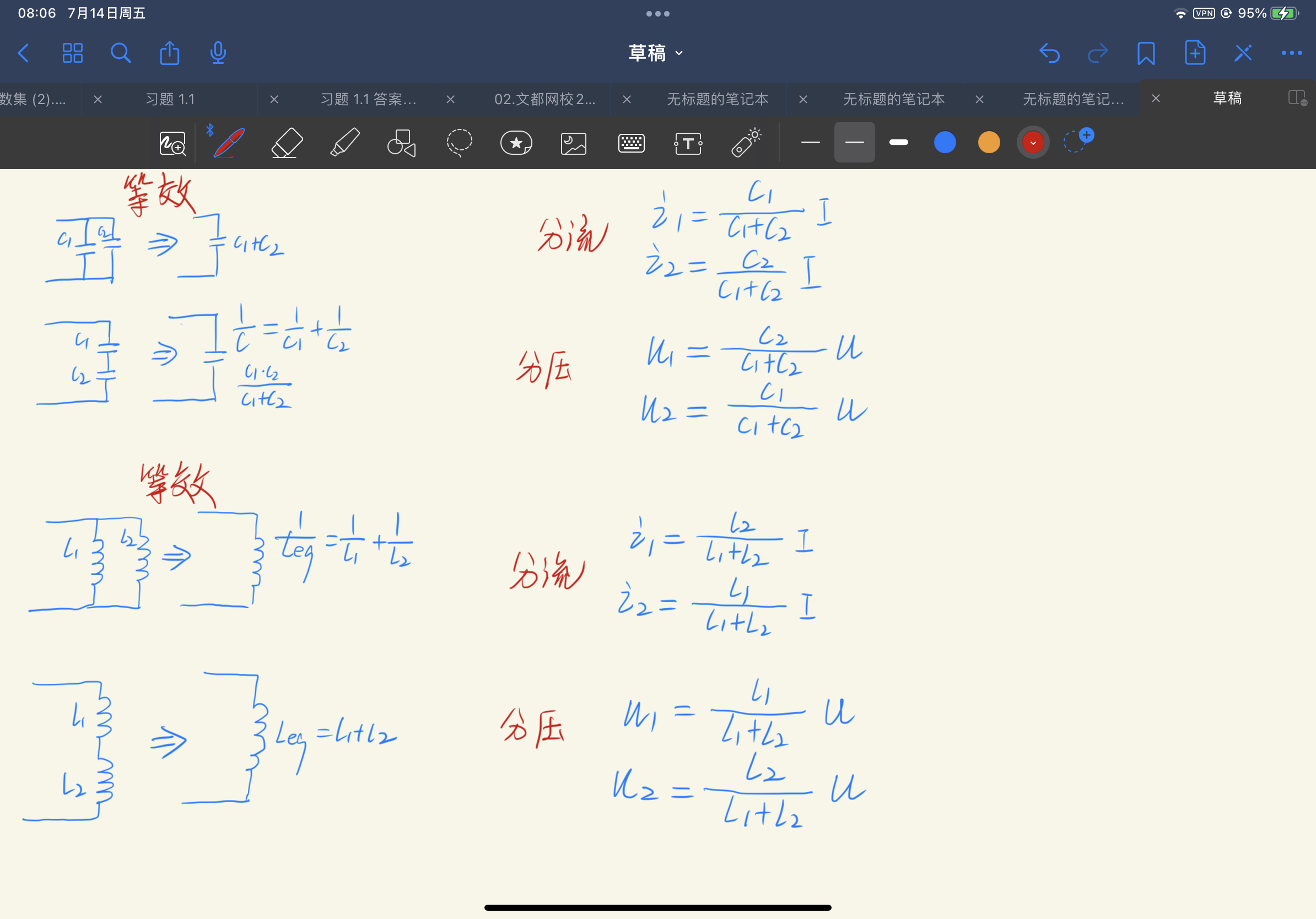
- 并联等效
- 并联等效电容:
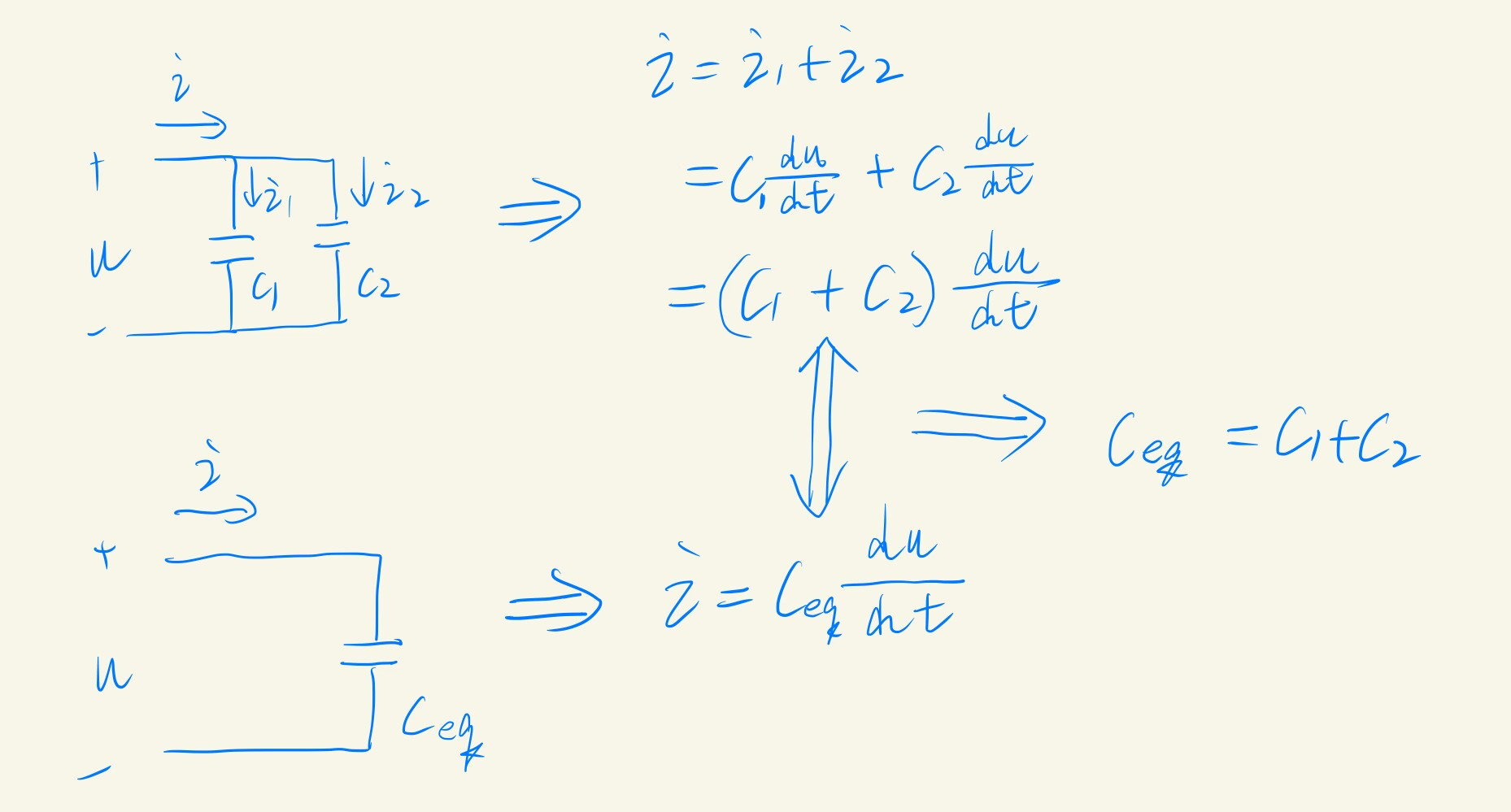
- 并联等效电容:
- 串联等效
- 串联等效电容:
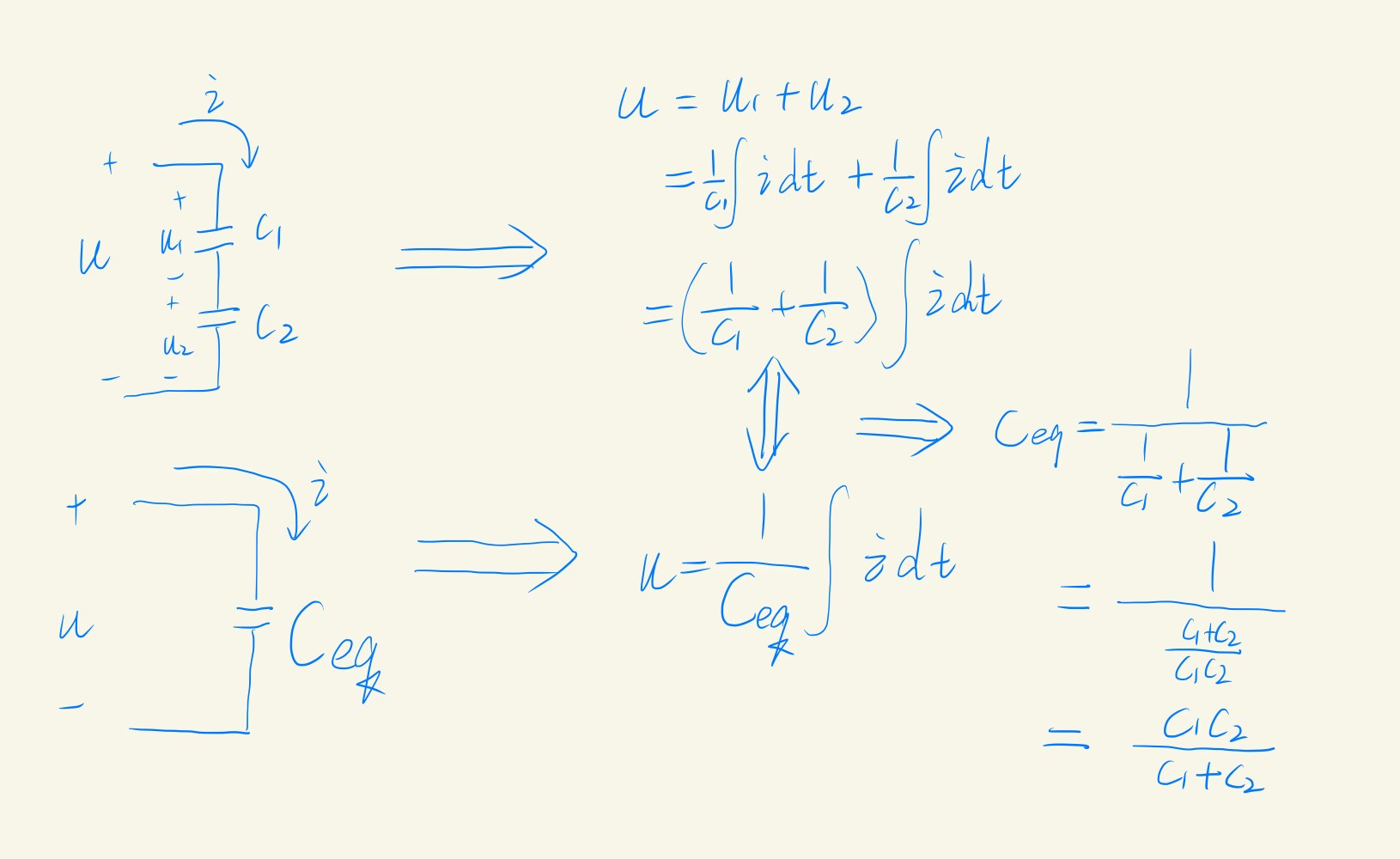
- 串联等效电容:
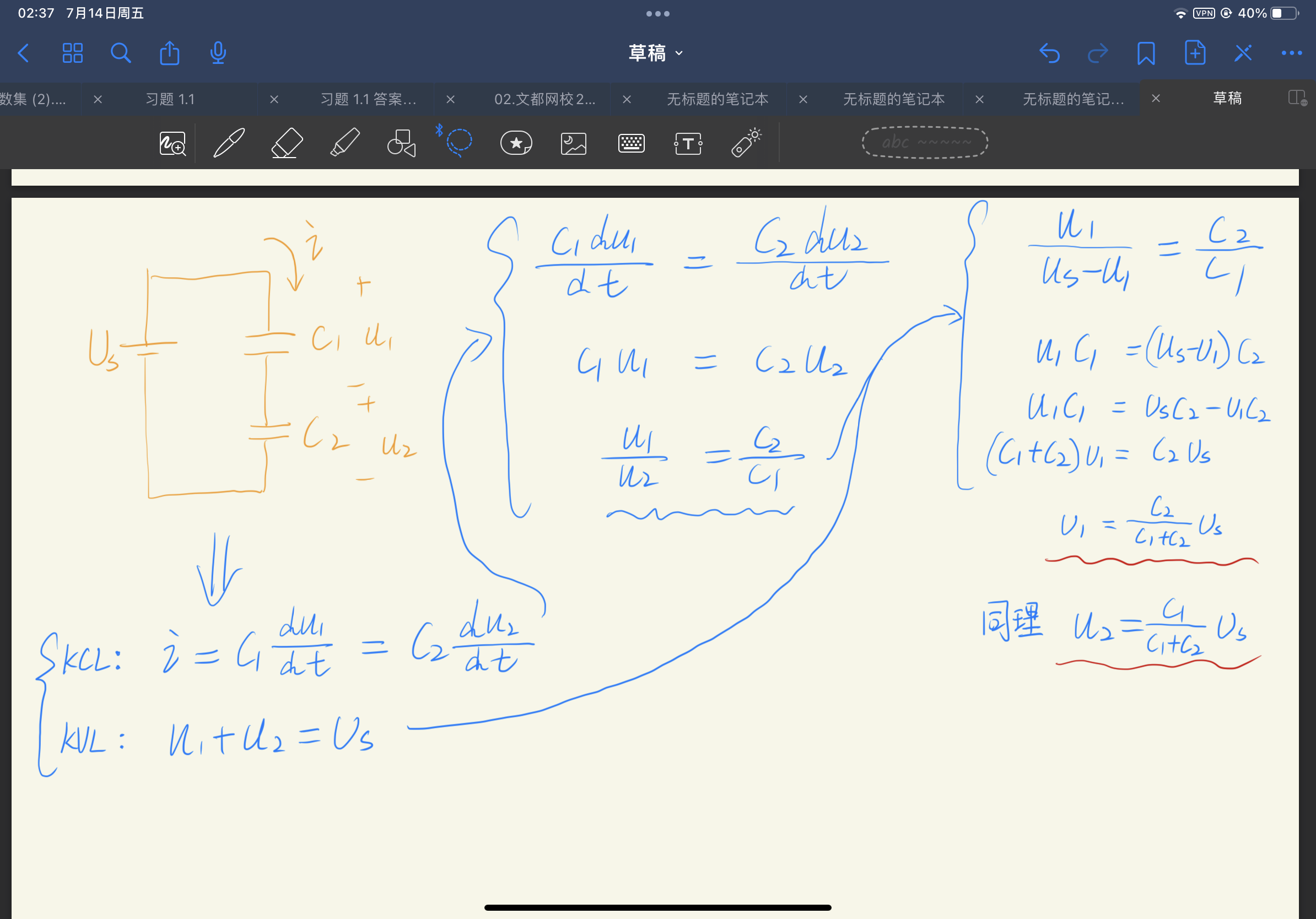
- 串联分压
- 利用KCL+KVL求解:
- 利用电荷守恒求解:
这种方法是求解含有多个电容电路的常用技巧
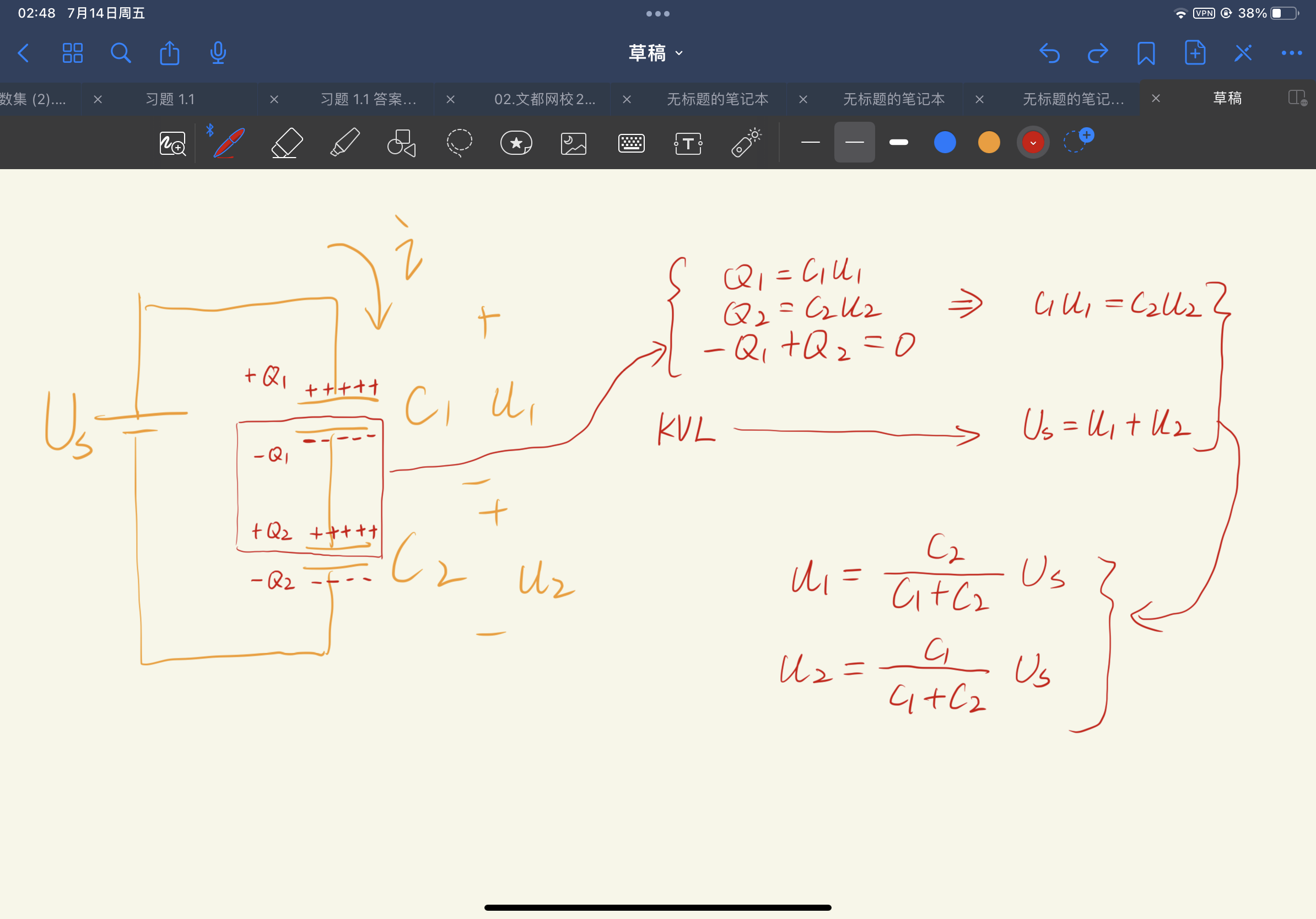
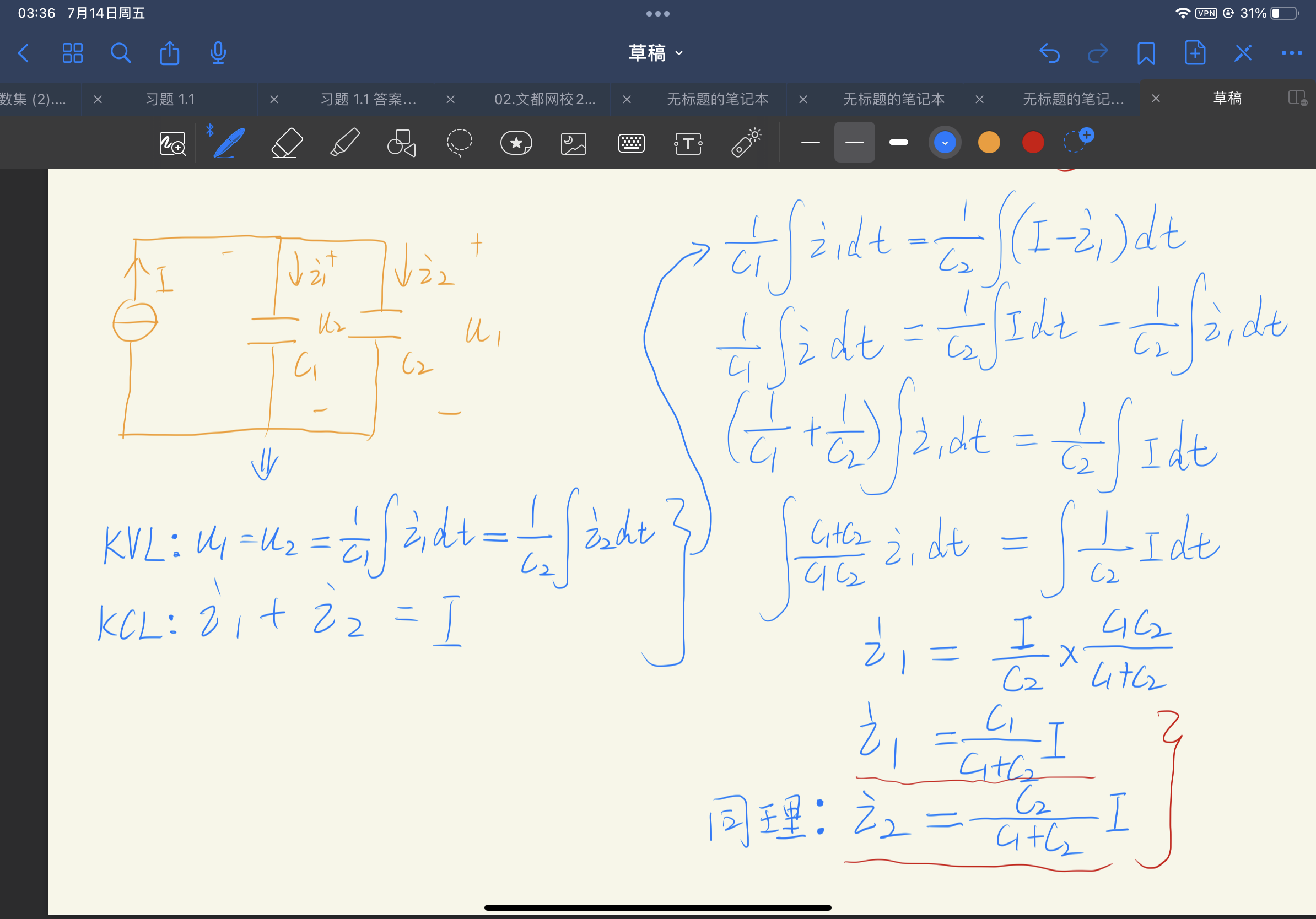
- 利用KCL+KVL求解:
- 并联分流
电感Inductors
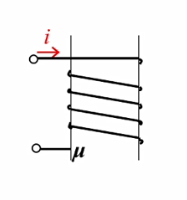
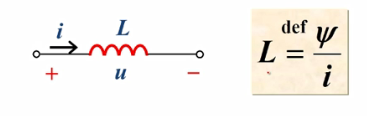
- 公式:
- 单位: H
- 其上电压
- 根据法拉第电磁感应定律:
- 又因为:
- 所以有:
- 可知i为常数时,u=0
- 根据法拉第电磁感应定律:
- 其上电流
- 可以根据其电压公式推导出来
- 和电容类似,可以得到:
- 吸收的功率
- 吸收的能量
- 假设负无穷到0时刻吸收的能量为0,即W(0)=0,则可得到:
- 由于
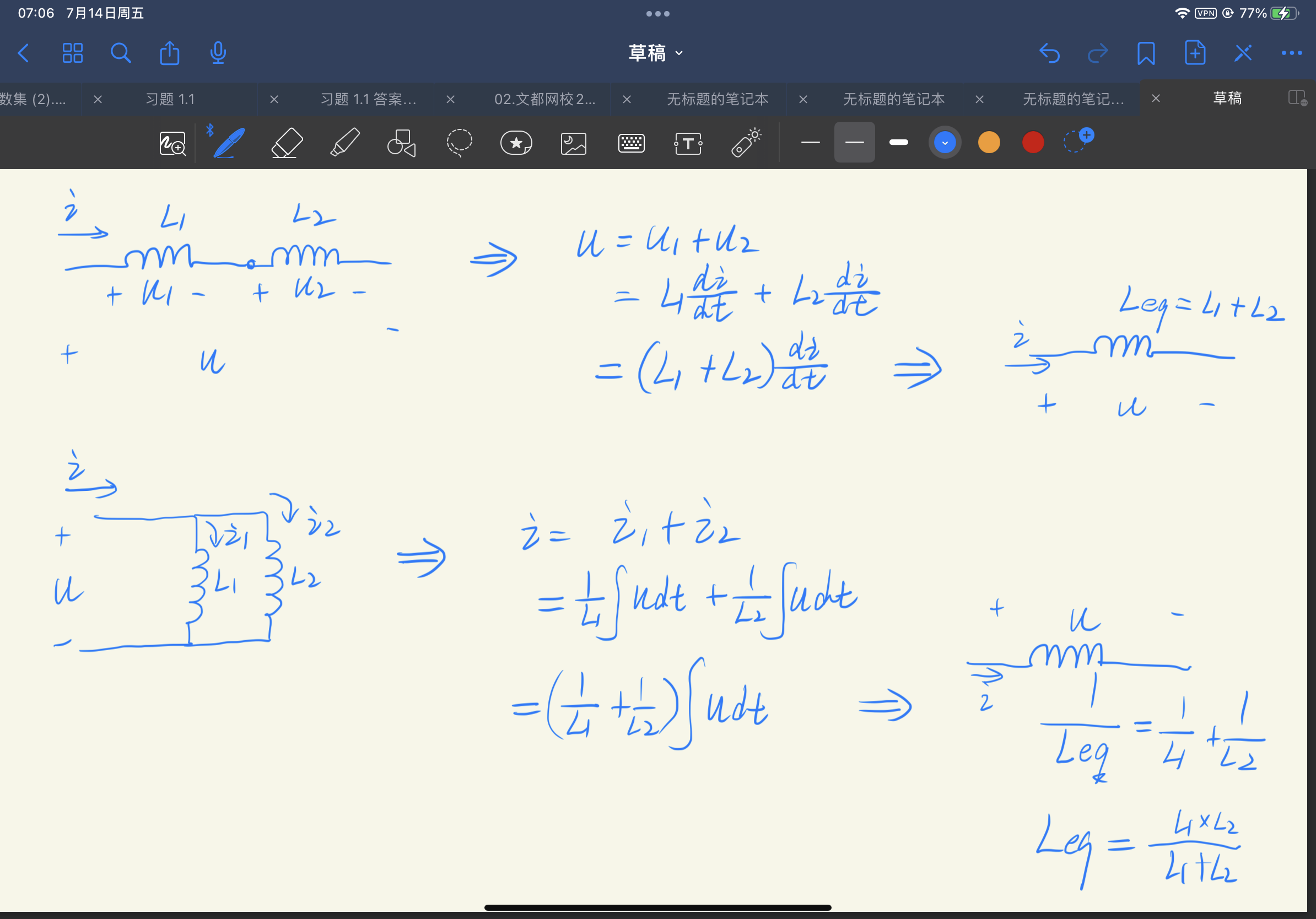
- 串联等效和并联等效
- 串联分压和并联分流
电容电感总结
忆阻器