一阶电路经典法

丁毅桂大约 3 分钟

一阶电路经典法

RC一阶电路

案例

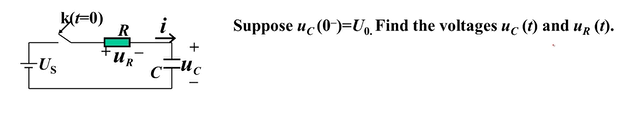
1.列写方程（拓扑约束+元件约束）

$u_R + u_c = U_s$
$u_R = iR$
$i = C\frac{d(u_c)}{dt}$

RC\frac{d(u_c)}{dt} + u_c = U_s

2.求解方程

齐次项的解

假设解的形式为 $u_c = Ae^{\lambda t}$
带入原方程得到特征方程: $RC\lambda + 1 = 0$
特征根: $\lambda = -\frac{1}{RC}$
微分方程的齐次通解：

u_c' = Ae^{\lambda t} = Ae^{-\frac{t}{RC}}

非齐次项的解

$U_s$ 是一个常数
显然可得微分方程的非齐次特解：

u_c''=U_s

通解=齐次通解+非齐次特解

\begin{align*} u_c&=u_c''+u_c' \\ &=U_s + Ae^{-\frac{t}{RC}} \end{align*}

3.确定初值

换路前： $u_c(0^-)=U_0$
换路后： $u_c(0^+)=u_c(0^-)=U_0$

4.确定系数

将 $u_c(0^+)=U_0$ 带入方程确定系数A:
$u_c = U_s + Ae^{-\frac{t}{RC}}$

t=0时：
$U_0 = U_s + Ae^{-\frac{0}{RC}}$
$U_0 = U_s + A$

得：

A=U_0-U_s

5.代入系数

u_c = U_s + (U_0-U_s)e^{-\frac{t}{RC}}

RC一阶电路的时间常数

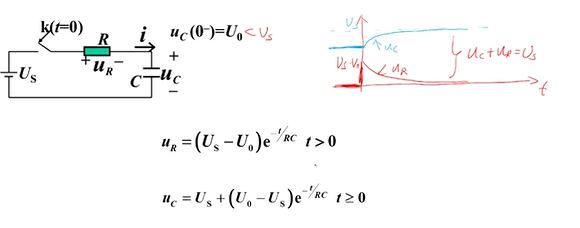
对RC一阶电路的两个支路量求解可以发现，
他们的指数项时相同的，意味着其变化速率也是相同的。
所以可以定义一个变量 $τ=RC$ 称RC一阶电路的时间常数，单位秒。

u_c = U_s + (U_0-U_s)e^{-\frac{t}{RC}}

u_c = U_s + (U_0-U_s)e^{-\frac{t}{τ}}

RL一阶电路

案例

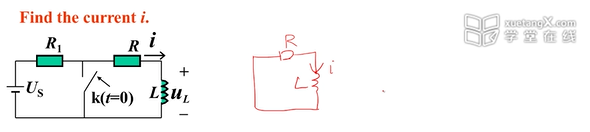
1.列写方程（拓扑约束+原件约束）

KVL

$-U_R = u_L$
$U_R = R*i$

元件约束

$u_L = L\frac{di}{dt}$

整理

\begin{align*} - Ri &= L\frac{di}{dt} \\ L\frac{di}{dt} - Ri &= 0 \\ \frac{L}{R}\frac{di}{dt} - i &= 0 \\ \end{align*}

2.求解方程

齐次项的解

假设解的形式为 $i_L = Ae^{\lambda t}$
带入原方程得到特征方程: $\frac{L}{R}\lambda + 1 = 0$
特征根: $\lambda = -\frac{1}{\frac{L}{R}}=-\frac{R}{L}$
齐次通解： $i_L = Ae^{\lambda t} = Ae^{-\frac{R}{L}t}$

3.确定初值

在t=0时刻，

$i(0)=i(0^+)=i(0^-)=\frac{U_s}{R_1+R}$

4.确定系数

\begin{align*} i_L &= Ae^{-\frac{R}{L}t} \\ A &= \frac{U_s}{R_1+R} \end{align*}

5.代入系数

i_L = \frac{U_s}{R_1+R}e^{-\frac{R}{L}t}

RL一阶电路的时间常数

i_L = \frac{U_s}{R_1+R}e^{-\frac{R}{L}t}

定义 $τ=\frac{L}{R}$ 称RL一阶电路的时间常数，单位秒。

i_L = \frac{U_s}{R_1+R}e^{-\frac{t}{τ}}

关于τ的讨论

工程观点

t=3τ， $e^{-\frac{t}{τ}}$ =0.05
t=5τ， $e^{-\frac{t}{τ}}$ =0.007
所以可以认为，经过3~5τ的时间后，电路的过度过程完全结束。

规律

τ越小，电路的过渡过程越快
τ越大，电路的过渡过程越慢

区别

$τ=RC$ R越大，τ越大，R增大的作用是减缓电容上电荷被中和的速度
$τ=\frac{L}{R}$ R越小，τ越大，R减小的作用是增大L的续流能力保持电感建立的磁场。

总结

一阶电路经典法求解

列写所关心支路量 $x(t)$ 的常微分方程（拓扑约束+原件约束）
根据换路定律，求 $x(0^+)$ 时刻的数值
求微分方程
- 方程是齐次微分方程，求其齐次通解
- 方程是非齐次微分方程，求其齐次通解+非齐次特解
通过 $x(0^+)$ 来确定齐次通解的待定系数