一阶电路三要素法

直观理解

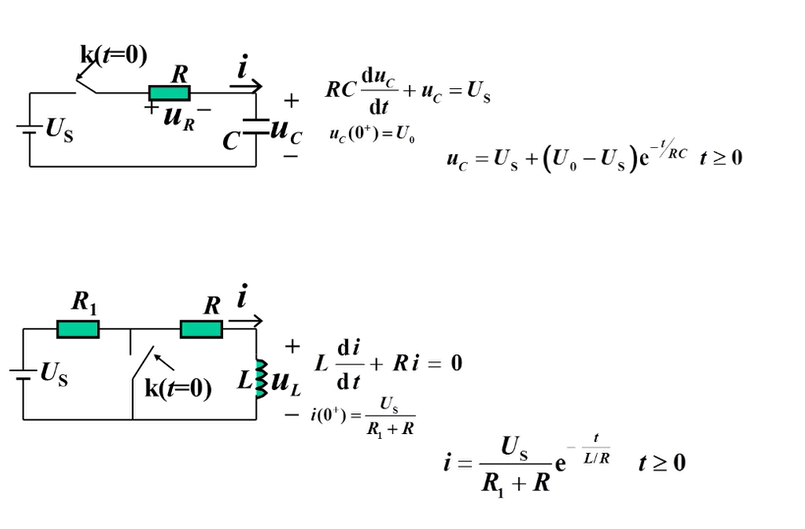
观察使用一阶电路经典法求解的支路量表达式的形式和参数特点。

当$R,L,C>0$ 时 $τ>0$时 表达式的指数项:

$$\lim\limits_{t \to 0} e^{-\frac{t}{τ}}=1$$

$$\lim\limits_{t \to +\infty} e^{-\frac{t}{τ}}=0$$

这意味着微分方程的非齐次特解为其稳态解

$$\begin{align*} \text{支路量$(t=+\infty)$} &= \text{稳态解} + A e^{-\frac{t}{τ}} \\ \text{支路量$(t=+\infty)$} &= \text{稳态解} + 0 \\ \end{align*}$$

齐次特解的待定系数

$$\begin{align*} \text{支路量($t=0^+$)} &= \text{稳态解} + A e^{-\frac{t}{τ}} \\ \text{支路量($t=0^+$)} &= \text{稳态解} + A \\ A &= \text{稳态解} - \text{支路量($t=0^+$)} \\ A &= \text{稳态解} - \text{初值} \end{align*}$$

所以

$$\text{支路量(t)} = \text{稳态解} + (\text{稳态解} - \text{初值}) e^{-\frac{t}{τ}}$$

数学理解

激励为常数X

考虑这样一个非齐次微分方程，X为常数。

$$\frac{du}{dt}+au=X \tag {a>0}$$

齐次通解

设

$$u'=Ae^{\lambda t}$$

则

$$\begin{align*} \frac{du}{dt}+au&=0 \\ A\lambda e^{\lambda t}+Aa e^{\lambda t}&=0 \\ \lambda +a&=0 \\ \lambda &=-a \end{align*}$$

得

$$u'=Ae^{-at}$$

非齐次特解

由于X为常数，所以设其非齐次特解是常数Y

$$u''=Y$$

则

$$\begin{align*} \frac{du}{dt}+au&=X \\ 0 + aY &= X \\ Y &= \frac{X}{a} \\ \end{align*}$$

得

$$u''=Y=\frac{X}{a}$$

微分方程通解

$$\begin{align*} u &= u'' + u' \\ u &= \frac{X}{a} + Ae^{-at} \\ \end{align*}$$

由于$a>0$,所以：

$$\begin{align*} \lim\limits_{t \to 0} Ae^{-at}&=1 \\ \lim\limits_{t \to +\infty} Ae^{-at}&=0 \end{align*}$$

所以有:

$$\begin{align*} \text{初值} = u(t=0) &= \frac{X}{a} + Ae^{-at} = \frac{X}{a} + A \\ \text{稳态} = u(t=+\infty) &= \frac{X}{a} + Ae^{-at} = \frac{X}{a}\\ A &= \text{初值}-\text{稳态}\\ \end{align*}$$

即

$$u(t) = \text{稳态} + (\text{初值}-\text{稳态})e^{-at}$$

激励为变量x(t)

对于

$$\frac{du}{dt}+au=x(t) \tag {a>0}$$

同样有

$$u(t) = \text{稳态(t)} + [\text{初值(t)}-\text{稳态(t)}]e^{-at}$$

只不过其稳态解和初值都是一个带t的表达式。

周期激励下动态电路的稳态解

例题1

T>>τ意味着电容可以在电压激励的一个周期T之内完成充电或放电的过度过程。

0~T 周期：

三要素

• $\text{初值}=0$
• $\text{稳态}=100$
• $τ=RC$

$$\begin{align*} u_c&=100+(0-100)e^{-\frac{t}{τ}} \\ &=100-100e^{-\frac{t}{τ}} \end{align*}$$

T~2T 周期：

三要素

• $\text{初值}=100$
• $\text{稳态}=0$
• $τ=RC$

$$\begin{align*} u_c&=0+(100-0)e^{-\frac{t}{τ}} \\ &=100e^{-\frac{t}{τ}} \end{align*}$$

结果

例题2

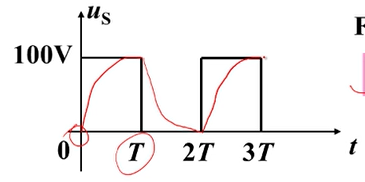
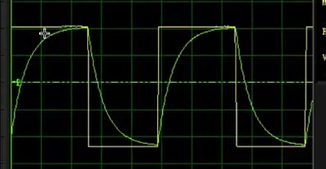
计算$u_c$的稳态电压

T is close to τ意味着电容无法在电压激励的一个周期之内完成过度过程

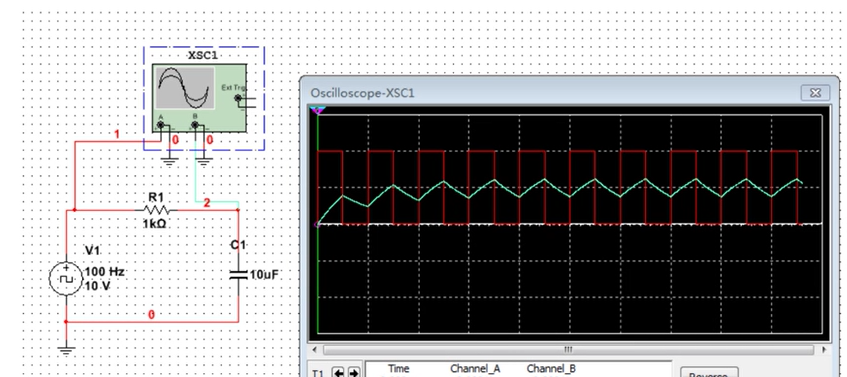
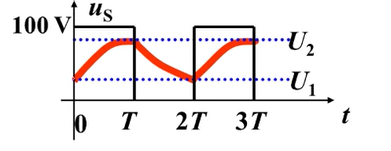
0~T 周期：

三要素

• $\text{初值}=U_1$
• $\text{稳态}=100$ (注意不是$U_2$)
• $τ=RC$

$$\begin{align*} u_c&=100+(U_1-100)e^{-\frac{t}{τ}} & t∈[0,T] \end{align*}$$

T~2T 周期：

三要素

• $\text{初值}=U_2$
• $\text{稳态}=0$ (注意不是$U_1$)
• $τ=RC$

$$\begin{align*} u_c&=0+(U_2-0)e^{-\frac{t}{τ}} \\ &=U_2e^{-\frac{t}{τ}} & t∈[0,T] \\ &=U_2e^{-\frac{t-T}{τ}} & t∈[T,2T] \end{align*}$$

联立得

$$u_c(t) = \begin{cases} 100+(U_1-100)e^{-\frac{t}{τ}} & t∈[0,T] \\ U_2e^{-\frac{t-T}{τ}} & t∈(T,2T]\\ \end{cases}$$

电路进入稳态后，将有：

$$\begin{cases} U_2 = u_c(1T) = 100+(U_1-100)e^{-\frac{1T}{τ}} \\ U_1 = u_c(2T) = U_2e^{-\frac{1T}{τ}} \\ \end{cases}$$

解之得：

$$\begin{cases} U_2 = 100 \cdot \frac{1}{1+e^{-\frac{T}{τ}}}\\ U_1 = 100 \cdot \frac{e^{-\frac{T}{τ}}}{1+e^{-\frac{T}{τ}}}\\ \end{cases}$$