动态电路

丁毅桂大约 4 分钟

什么是动态电路？

电阻电路： 元件上的支路量随着激励的改变而瞬时(理想情况下)改变
动态电路：
- 电容/电感为储能元件，
- 能量的变化不可能瞬时的(电场/磁场的建立/消散都需要时间)，
- 表征其储能的电容电压和电感电流必须随时间变化。
- 所谓动态就是储能元件上的能量随时间改变的过程。

动态电路的过度过程

过度过程（暂态过程）是什么

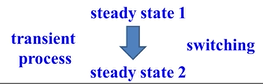
稳态1==换路==>稳态2
=======暂态=======

产生过度过程的两个根本条件

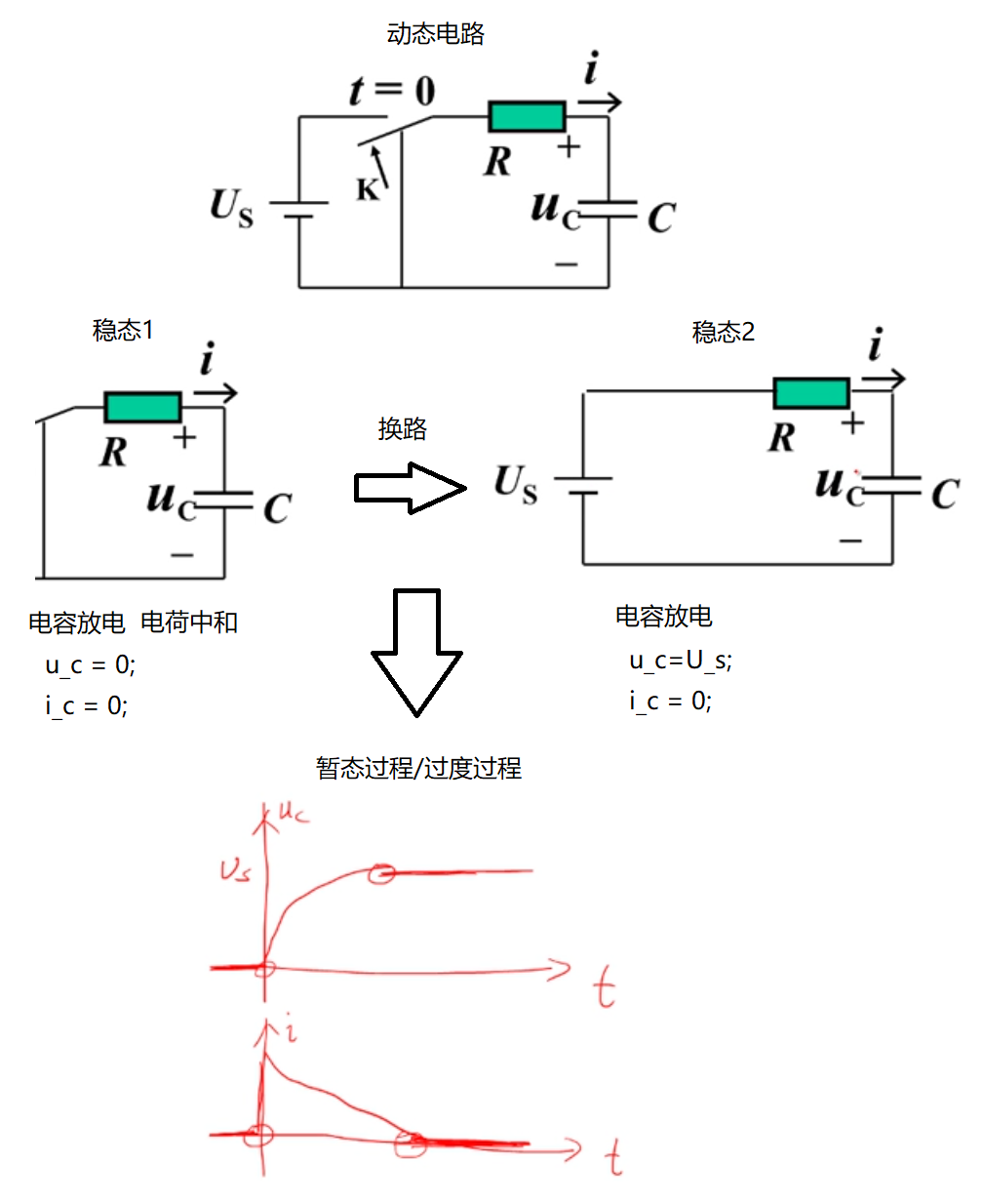
列写方程的两个基本要素：元件约束 + 拓扑约束

阶数

如果一个电路所对应的方程是一阶(/二阶)微分方程，那么这个电路就叫做一阶(/二阶)电路

一阶电路一阶方程

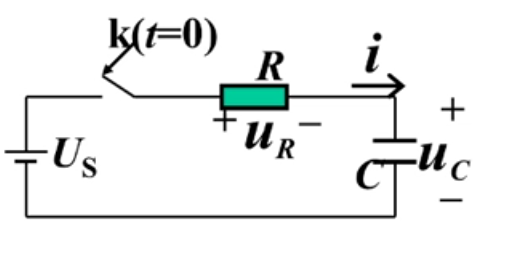
KVL拓扑约束 + RC元件约束:

\begin{align*} KVL&: U_s = u_r + u_c \\ R&: U_r =Ri \\ C&: i = C \frac{du_c}{dt} \\ \end{align*}

元件约束代入KVL:

\begin{align*} U_s &= u_r + u_c \\ U_s &= RC\frac{du_c}{dt} + u_c \\ \end{align*}

化微分项系数为1：

\frac{du_c}{dt} + \frac{1}{RC} u_c = \frac{1}{RC} U_s

二阶电路二阶方程

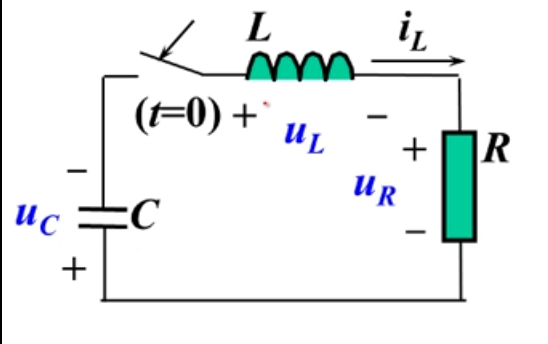
KVL拓扑约束+RLC元件约束:

\begin{align*} KVL&: u_C + u_L + u_R = 0 \\ C&: i = C \frac{du_C}{dt} \\ L&: u = L\frac{di}{dt} \\ R&: U_r = Ri \\ \end{align*}

元件约束代入KVL:

\begin{align*} u_C + u_L + u_R = 0 \\ u_C + L * \frac{d(i=C\frac{du_C}{dt})}{dt}+ R * (i=C\frac{du_C}{dt})=0\\ u_C + LC\frac{d^2(u_C)}{dt}+ RC\frac{du_C}{dt}=0 \\ \end{align*}

化微分项系数为1：

\frac{d^2(u_C)}{dt}+ \frac{R}{L}\frac{du_C}{dt} + \frac{1}{LC}u_C=0 \\

\frac{df(t)}{dt} + 2f(t) = 0

思考

\frac{df(t)}{dt} + 2f(t) = t^2

可以把原方程看成是： $\frac{df(t)}{dt} + 2f(t) = 0 + t^2$
非齐次方程通解 = 齐次方程通解 + 非齐次方程特解
齐次方程通解： $f_a(t) = A e^{-2 t}$ 可使得方程右边为0
非齐次方程特解：
- 因为二次多项式函数的导数是二次多项式
- 所以，设其为 $f_b(t) = Bt^2 + Ct + D$
- 则导数为 $f_b'(t) = 2Bt + C + 0$
- 代入原方程 $\frac{df(t)}{dt} + 2f(t) = t^2$ $\frac{df ( t )}{d t} + 2 f (t) = t^{2}$ 得：
  - $2Bt + C + 2*(Bt^2 + Ct + D) = t^2$
  - $2Bt + C + 2Bt^2 + 2Ct + 2D = t^2$
  - $(2B)t^2 + (2C+2B)t + (2D + C)= t^2$ $(2 B) t^{2} + (2 C + 2 B) t + (2 D + C) = t^{2}$
    - $2B=1$
    - $B=0.5$
    - $2C+2B=0$
    - $C=-0.5$
    - $2D+C=0$
    - $D=0.25$
  - $f_b(t) = 0.5t^2-0.5t+0.25$
- 特解使得方程右边为 $t^2$
非齐次方程通解 = 齐次方程通解 + 非齐次方程特解
- $f(t)=f_a(t)+f_b(t)$
- $= Ae^{-2 t} + 0.5t^2-0.5t+0.25$
如果：
- 有系统初始条件f(0)=1 则可计算得：A=0.75

[2 第47讲动态电路(Dynamic Circuits)(3)]

动态电路的暂态过程如何求解？