零输入响应和零状态响应

几种不同的视角

电路的非齐次常系数线性常微分方程

纯数学角度：

$$\text{全解}=\text{通解}+\text{特解}$$

一阶电路经典法角度：

$$\text{全响应}=\text{自然响应}+\text{强制响应}$$

一阶电路三要素法角度：

$$\text{全响应}=\text{自然响应}+\text{稳态}$$

零输入响应和零状态响应角度：

$$\text{全响应}=\text{零输入响应}+\text{零状态响应}$$

案例

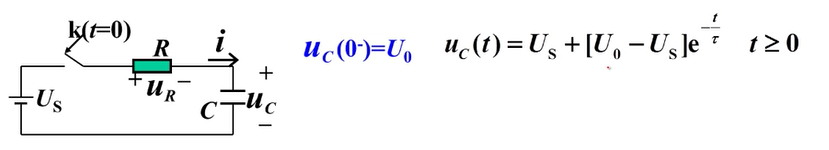
零状态响应

独立源作用，储能元件不作用（零状态、无初值）

$$\begin{align*} u_c'&=\text{稳态}+(\text{初值}-\text{稳态})e^{-\frac{t}{τ}} \\ u_c'&=U_s+(0-U_s)e^{-\frac{t}{τ}} \end{align*}$$

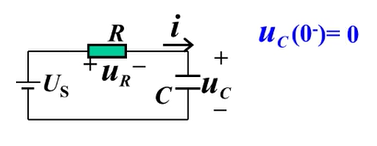
零输入响应

储能元件作用（有初值），独立源不作用

$$\begin{align*} u_c''&=\text{稳态}+(\text{初值}-\text{稳态})e^{-\frac{t}{τ}} \\ u_c''&=0+(U_0-0)e^{-\frac{t}{τ}} \\ u_c''&=U_0e^{-\frac{t}{τ}} \end{align*}$$

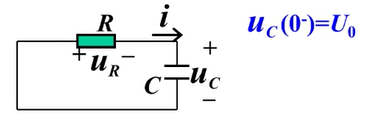
全响应

$$\begin{align*} u_c&=u_c'+u_c'' \\ &=U_s+(0-U_s)e^{-\frac{t}{τ}}+U_0e^{-\frac{t}{τ}} \\ &=U_s+(U_0-U_s)e^{-\frac{t}{τ}} \end{align*}$$

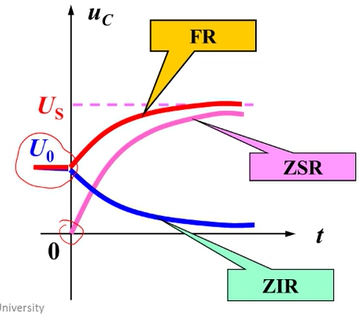
本质

• 叠加定理。
• 把一个既有独立源作用，又有带初值储能原件作用的电路，
• 看成是他们分别作用的叠加。

优点

• 在零状态下，储能原件的电压电流的微分、积分关系是线性关系。
• 当其电压电流关系为线性关系时，就可以使用叠加定理进行分析和求解

电容

电容上的电流和电压是线性微分关系：

$$i=C\frac{du}{dt}$$

电容上的电压和电流不是是线性微分关系

$$u(t)=u(0)+\frac{1}{C}∫_0^t iτ$$

但在零状态情况下(电容无储能，初值为0),
则电压和电流的关系是线性积分关系：

$$\begin{align*} u(t)&=u(0)+\frac{1}{C}∫_0^t i(t)τ \\ &=0+\frac{1}{C}∫_0^t i(t)τ \\ &=\frac{1}{C}∫_0^t i(t)τ \\ \end{align*}$$

电感

电感上电压和电流是线性微分关系

$$u=L\frac{di}{dt}$$

零状态条件下，电感上电流和电压是线性积分关系

$$\begin{align*} i(t)&=i(0)+\frac{1}{L}∫_0^t u(t)τ \\ &=0+\frac{1}{L}∫_0^t u(t)τ \\ &=\frac{1}{L}∫_0^t u(t)τ \\ \end{align*}$$

示例

零状态条件下，激励和响应是线性关系

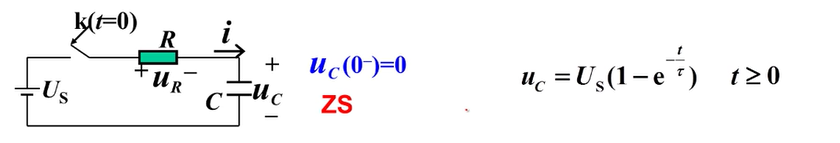
用处

可以先求解电路的零状态单位冲激响应，然后将其与激励进行卷积积分，从而求解任意激励下的零状态响应。